Burgerlar tenglamasi - Burgers equation - Wikipedia
Burgerlar tenglamasi yoki Betmen - Burgerlar tenglamasi bu asosdir qisman differentsial tenglama ning turli sohalarida uchraydi amaliy matematika, kabi suyuqlik mexanikasi,[1] nochiziqli akustika,[2] gaz dinamikasi va transport oqimi. Tenglama birinchi tomonidan kiritilgan Garri Beytmen 1915 yilda[3][4] va keyinchalik tomonidan o'rganilgan Johannes Martinus Burgers 1948 yilda.[5]
Berilgan maydon uchun va diffuziya koeffitsienti (yoki kinematik yopishqoqlik, asl suyuqlik mexanik kontekstida bo'lgani kabi) , Burgerlar tenglamasining umumiy shakli (shuningdek, ma'lum yopishqoq burgerlar tenglamasi) bitta bo'shliq o'lchamida dissipativ tizim:
Diffuziya muddati yo'q bo'lganda (ya'ni. ), Burgerlar tenglamasi noaniq burgerlar tenglamasi:
prototipi bo'lgan saqlanish tenglamalari uzilishlarni rivojlanishi mumkin (zarba to'lqinlari ). Oldingi tenglama advektiv shakl Burgerlar tenglamasi. The konservativ shakl raqamli integralda ko'proq foydali ekanligi aniqlandi
Shartlarni tushuntirish
Burgerlar tenglamasida 4 ta shart mavjud: va . Bir fazoviy harakatlanuvchi yopishqoq suyuqlikdan iborat tizimda () va bitta vaqtinchalik () o'lchov, masalan. ichidan suyuqlik o'tadigan ingichka ideal truba, Burgers tenglamasi vaqt o'tishi bilan quvur bo'ylab har bir joyda suyuqlik tezligini tavsiflaydi. Tenglama shartlari quyidagi miqdorlarni ifodalaydi:[6]
- : fazoviy koordinata
- : vaqtinchalik koordinata
- : ko'rsatilgan fazoviy va vaqtinchalik koordinatalarda suyuqlik tezligi
- : suyuqlikning yopishqoqligi
Qovushqoqlik suyuqlikning doimiy jismoniy xususiyati bo'lib, boshqa atamalar bu yopishqoqlikka bog'liq bo'lgan dinamikani anglatadi.
Inviscid Burgers tenglamasi
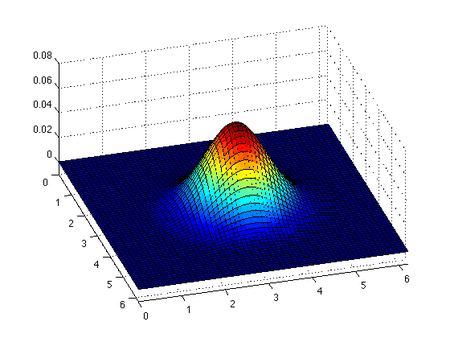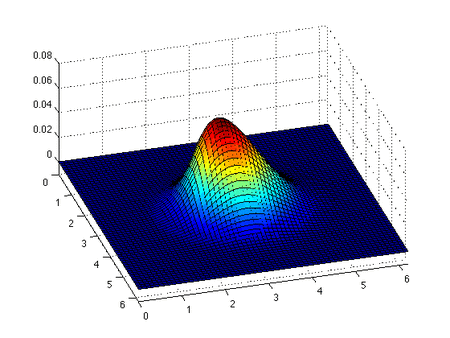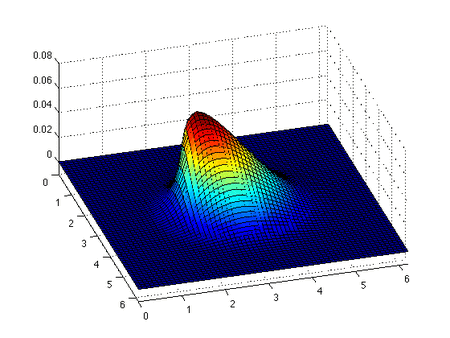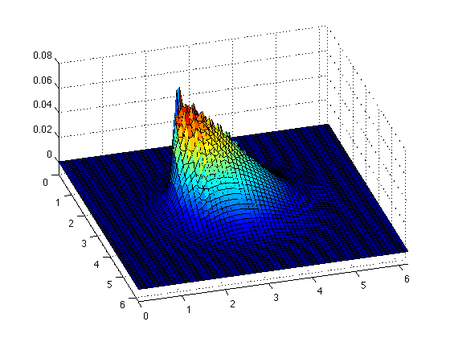
Invisiscid Burgers tenglamasi a saqlanish tenglamasi, umuman olganda birinchi tartibli kvazilinear giperbolik tenglama. Tenglamaning echimi va boshlang'ich shart bilan birga
tomonidan qurilishi mumkin xarakteristikalar usuli. Xarakterli tenglamalar
Ikkinchi tenglamaning integratsiyasi shundan dalolat beradi xarakteristikasi bo'yicha doimiy va birinchi tenglamaning integrali shuni ko'rsatadiki, xususiyatlar to'g'ri chiziqlardir, ya'ni.
qayerda ning nuqtasi (yoki parametri) x-aksis (t = 0) ning x-t xarakterli egri chizilgan tekislik. Nuqtada tezlik dastlabki holatdan ma'lum va shu nuqtadan kelib chiqadigan xarakteristikada harakatlanayotganda bu qiymat o'zgarmas ekan, biz yozamiz bu xususiyat bo'yicha. Shuning uchun, ushbu xarakteristikaning traektoriyasi
Shunday qilib, eritma tomonidan beriladi
Bu noaniq munosabatlar, inviscid Burgers tenglamasining echimini belgilaydi, agar xarakteristikalar kesishmasa. Agar xarakteristikalar kesishgan bo'lsa, unda PDE uchun klassik echim mavjud emas va a hosil bo'lishiga olib keladi zarba to'lqini. Aslida buzilish vaqti oldin zarba to'lqini hosil bo'lishi mumkin
Chiziqli boshlang'ich shart uchun Inviscid Burgers tenglamasi
Subrahmanyan Chandrasekhar 1943 yilda dastlabki shart chiziqli bo'lganda aniq echimni taqdim etdi, ya'ni. , bu erda a va b doimiylar.[7] Aniq echim
Ushbu echim ham to'liq integral noaniq burgerlar tenglamasining sababi, chunki u tenglamada paydo bo'ladigan mustaqil o'zgaruvchilar sonining qancha o'zboshimchalik doimiyligini o'z ichiga oladi.[8][yaxshiroq manba kerak ] Boshqa tegishli dastlabki shartlar uchun aniq echimlar, umuman, ma'lum emas.
Viskoz burgerlar tenglamasi

Yopishqoq burgerlar tenglamasini ning yordamida chiziqli tenglamaga aylantirish mumkin Koul-Xopf transformatsiyasi [9][10]
bu uni tenglamaga aylantiradi
ga nisbatan birlashtirilishi mumkin olish
qayerda chegara shartlariga bog'liq bo'lgan funktsiya. Agar bir xil (masalan, davriy domenda muammo hal etilishi kerak bo'lsa), biz quyidagini olamiz diffuziya tenglamasi
Burgerlar tenglamasiga yechim topish uchun diffuziya tenglamasini echish va Kole-Xopf konvertatsiyasini teskari aylantirish mumkin:
Boshqa shakllar
Umumlashtirilgan burgerlar tenglamasi
Umumlashtirilgan Burgerlar tenglamasi kvazilinear konvektivni ko'proq umumlashtirilgan shaklga uzatadi, ya'ni.
qayerda u ning har qanday ixtiyoriy funktsiyasi. Invisid tenglama hali uchun kvazilinear giperbolik tenglama va uning echimi yordamida qurish mumkin xarakteristikalar usuli oldingi kabi.[11]
Stoxastik burgerlar tenglamasi
Joy-vaqt shovqini qo'shildi stoxastik Burgerlar tenglamasini hosil qiladi[12]
Ushbu stoxastik PDE bir o'lchovli versiyasidir Kardar - Parisi - Chjan tenglamasi dalada almashtirish bilan .
Shuningdek qarang
Adabiyotlar
- ^ Bu bosim muddati o'chirilgan Navier-Stokes momentum tenglamasiga taalluqlidirBurgerlar tenglamasi (PDF): bu erda o'zgaruvchi oqim tezligi y = u
- ^ Bu kelib chiqadi Vestervelt tenglamasi qat'iy ravishda oldinga siljiydigan to'lqinlar va kechiktirilgan vaqt doirasiga koordinatali transformatsiyani qo'llash bilan: bu erda o'zgaruvchi bosim
- ^ Bateman, H. (1915). Suyuqliklar harakati bo'yicha ba'zi so'nggi tadqiqotlar. Oylik ob-havo sharhi, 43 (4), 163-170.
- ^ Whitham, G. B. (2011). Lineer va nochiziqli to'lqinlar (42-jild). John Wiley & Sons.
- ^ Burgerlar, J. M. (1948). Turbulentlik nazariyasini aks ettiruvchi matematik model. Amaliy mexanikadagi yutuqlarda (1-jild, 171-199-betlar). Elsevier.
- ^ Kemeron, Mariya. "BURJERLARNING TEXNIKASI HAQIDA QAYDLAR" (PDF).
- ^ Chandrasekhar, S. (1943). "Samolyot zarba to'lqinlarining parchalanishi to'g'risida "(№ 423). Balistik tadqiqot laboratoriyalari. Iqtibos jurnali talab qiladi
| jurnal =(Yordam bering) - ^ Forsit, A. R. (1903). Differentsial tenglamalar haqida risola. London: Makmillan.
- ^ Julian Koul (1951). Aerodinamikada yuzaga keladigan kvazi chiziqli parabolik tenglamada. Amaliy matematikaning chorakligi, 9 (3), 225-236.
- ^ Eberxard Xopf (1950 yil sentyabr). "Qisman differentsial tenglama ut + uux = muxx". Sof va amaliy matematika bo'yicha aloqa. 3 (3): 201–230. doi:10.1002 / cpa.3160030302. hdl:10338.dmlcz / 102083.
- ^ Courant, R., and Hilbert, D. Matematik fizika usullari. Vol. II.
- ^ Vang, V.; Roberts, A. J. (2015). "Burgerlar tenglamasida stoxastik qo'shilishning o'ziga o'xshashligi uchun diffuziya yaqinlashishi". Matematik fizikadagi aloqalar. 333: 1287–1316. doi:10.1007 / s00220-014-2117-7.
Tashqi havolalar
- Burgerlar tenglamasi EqWorld-da: Matematik tenglamalar olami.
- Burgerlar tenglamasi NEQwiki-da, chiziqli bo'lmagan tenglamalar ensiklopediyasi.
- Burgerlar tenglamasi Wolfram | Alpha qidiruv natijalari.



























![{ displaystyle u (x, t) = - 2 nu { frac { qismli} { qisman x}} ln chap {(4 pi nu t) ^ {- 1/2} int _ {- infty} ^ { infty} exp left [- { frac {(x-x ') ^ {2}} {4 nu t}} - { frac {1} {2 nu }} int _ {0} ^ {x '} f (x' ') dx' ' right] dx' right }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c946a41e496bc7244b0dd06c8ab232998984f6e9)






