Maksimal subarray muammosi - Maximum subarray problem

Namunaning boshlang'ich va oxirgi pozitsiyalari asosida sub-massivlarning qanday o'zgarishini ingl. Har bir mumkin bo'lgan qo'shni sub-qator rangli chiziqdagi nuqta bilan ifodalanadi. Ushbu nuqtaning y koordinatasi namunaning yig'indisini bildiradi. Uning x-koordinatasi namunaning oxirini, shu rangli chiziqdagi eng chap nuqta esa namunaning boshlanishini bildiradi. Bunday holda, namunalar olinadigan massiv [2, 3, -1, -20, 5, 10].

Yilda Kompyuter fanlari, maksimal summa subarray muammosi ma'lum bir o'lchovli ichida eng katta yig'indisi bilan qo'shni subarrayni topish vazifasi qator A [1 ... n] raqamlar. Rasmiy ravishda, indekslarni topish vazifasi ${displaystyle i}$ va ${displaystyle j}$ bilan ${displaystyle 1leq bilan jleq n}$ , shuncha summa

{displaystyle sum _ {x = i} ^ {j} A [x]}

imkon qadar katta. (Muammoning ba'zi bir formulalari, shuningdek, bo'sh subarrayni ko'rib chiqishga imkon beradi; konventsiya bo'yicha, bo'sh subarrayning barcha qiymatlari yig'indisi nolga teng.) Kirish massividagi har bir raqam ijobiy, salbiy yoki nolga teng bo'lishi mumkin.^[1]

Masalan, [-2, 1, -3, 4, -1, 2, 1, -5, 4] qiymatlar massivi uchun eng katta yig'indisi bo'lgan qo'shni subarray [4, -1, 2, 1] , 6 sum bilan.

Ushbu muammoning ba'zi xususiyatlari:

Agar massivda barcha manfiy bo'lmagan sonlar bo'lsa, unda muammo ahamiyatsiz bo'ladi; maksimal subarray butun massivdir.
Agar massivda barcha ijobiy bo'lmagan sonlar bo'lsa, u holda massivning maksimal qiymatini o'z ichiga olgan 1-o'lchamdagi har qanday subarray (yoki ruxsat berilgan bo'lsa, bo'sh subarray) bo'ladi.
Bir nechta turli kichik massivlar bir xil maksimal summaga ega bo'lishi mumkin.

Ushbu muammoni turli xil algoritmik usullar, shu jumladan qo'pol kuch,^[2] bo'ling va zabt eting,^[3] dinamik dasturlash,^[4] va eng qisqa yo'llarga qisqartirish.^{[iqtibos kerak ]}

Tarix

Maksimal subarray muammosi tomonidan taklif qilingan Ulf Grenander uchun soddalashtirilgan model sifatida 1977 yilda maksimal ehtimollik raqamlashtirilgan tasvirlardagi naqshlarni baholash.^[5]

Grenander haqiqiy sonlarning ikki o'lchovli massivida maksimal yig'indisi bo'lgan to'rtburchaklar subarray topmoqchi edi. Ikki o'lchovli muammo uchun qo'pol kuch algoritmi ishlaydi O(n⁶) vaqt; chunki bu juda sekin edi, Grenander uning tuzilishi haqida tushuncha olish uchun bir o'lchovli muammoni taklif qildi. Grenander bir o'lchovli masalani echadigan algoritmni keltirdi O(n²) vaqt,^[1-eslatma]qo'pol kuchning ishlash vaqtini yaxshilash O(n³). Qachon Maykl Shamos muammo haqida eshitdi, u bir kechada an O(n jurnal n) ajratish va bosib olish algoritmi Ko'p o'tmay, Shamos bir o'lchovli muammoni va uning tarixini a da tasvirlab berdi Karnegi Mellon universiteti ishtirok etgan seminar Jey Kadane, kim bir daqiqada ishlab chiqardi O(n) vaqt algoritmi,^[5]^[6]^[7] bu imkon qadar tezroq.^[2-eslatma] 1982 yilda, Devid Gris xuddi shu narsani qo'lga kiritdi O(n) qo'llash orqali vaqt algoritmi Dijkstra "standart strategiya";^[8] 1989 yilda, Richard Bird dan foydalanib qo'pol kuch algoritmini sof algebraik manipulyatsiya qilish orqali olingan Bird – Meertens formalizmi.^[9]

Grenanderning ikki o'lchovli umumlashmasi O (n³) vaqtni Kadane algoritmidan subroutin sifatida foydalanish yoki bo'linish va yutish yondashuvi orqali. Biroz tezroq algoritmlar asosida masofa matritsasini ko'paytirish tomonidan taklif qilingan Tamaki va Tokuyama (1998) va tomonidan Takaoka (2002). Hech qanday tezkor algoritm mavjud emasligiga ba'zi dalillar mavjud; ikki o'lchovli maksimal subarray masalasini O da echadigan algoritm (n^{3 "}) har qanday ε> 0 uchun vaqt xuddi shunday tezkor algoritmni bildiradi barcha juftliklar eng qisqa yo'llar muammo.^[10]

Ilovalar

Maksimal subarray muammolari ko'plab sohalarda paydo bo'ladi, masalan, genomik ketma-ketlikni tahlil qilish va kompyuterni ko'rish.

Genomik ketma-ketlikni tahlil qilish oqsillar ketma-ketligining muhim biologik segmentlarini aniqlash uchun maksimal subarray algoritmlaridan foydalanadi.^{[iqtibos kerak ]} Ushbu muammolarga konservalangan segmentlar, GC ga boy mintaqalar, tandem takrorlanishi, murakkabligi past filtr, DNK bilan bog'lanish sohalari va yuqori zaryadli hududlar kiradi.^{[iqtibos kerak ]}

Yilda kompyuterni ko'rish, rasmdagi eng yorqin maydonni aniqlash uchun bitmap rasmlarda maksimal subarray algoritmlaridan foydalaniladi.

Kadanening algoritmi

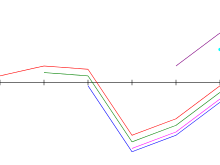
Misol yugurish
Kadane algoritmini yuqorida misol qatori. Moviy: eng katta yig'indisi bilan tugaydigan subarray men; yashil: hozirgacha duch kelgan eng katta summa bilan subarray; kichik harf bo'sh qatorni bildiradi; o'zgaruvchan men Python kodida yashirin qoldirilgan.

Kadanening algoritm berilgan massivni skanerdan o'tkazadi ${displaystyle A [1ldots n]}$ chapdan o'ngga In ${displaystyle j}$ qadam, u subarrayni eng katta yig'indisi bilan tugashini hisoblab chiqadi ${displaystyle j}$ ; ushbu summa o'zgaruvchida saqlanadi joriy_sum.^[3-eslatma]Bundan tashqari, u subarreani har qanday joyda eng katta summa bilan hisoblab chiqadi ${displaystyle A [1ldots j]}$ , o'zgaruvchan holda saqlanadi best_sum,^[4-eslatma]va ning barcha qiymatlari maksimal darajada osonlik bilan olinadi joriy_sum hozirgacha ko'rilgan, qarang algoritmning 7-chizig'i.

Kabi halqa o'zgarmas, ichida ${displaystyle j}$ qadimgi qadriyat joriy_sum hamma uchun maksimal darajada ushlab turadi ${displaystyle iin {1, ldots, j}}$ summaning ${displaystyle A [i] + cdots + A [j-1]}$ .^[5-eslatma]Shuning uchun, joriy_sum ${displaystyle + A [j]}$ ^[6-eslatma]hamma uchun maksimal hisoblanadi ${displaystyle iin {1, ldots, j}}$ summaning ${displaystyle A [i] + cdots + A [j]}$ . Keyingi maksimalni kengaytirish uchun ishni ham qamrab oling ${displaystyle i = j + 1}$ , bo'sh subarrayni ham ko'rib chiqish kifoya ${displaystyle A [j + 1; ldots; j]}$ . Bu 6-qatorda tayinlash orqali amalga oshiriladi ${displaystyle max (0,}$ joriy_sum ${displaystyle + A [j])}$ ning yangi qiymati sifatida joriy_sum, bundan keyin hamma maksimal darajada ushlab turadi ${displaystyle iin {1, ldots, j + 1}}$ summaning ${displaystyle A [i] + cdots + A [j]}$ .

Shunday qilib, muammoni quyidagi kod bilan hal qilish mumkin,^[4]^[7] bu erda ifodalangan Python:

1 def max_subarray(raqamlar):2     "" "Har qanday qo'shni subarrayning eng katta yig'indisini toping." ""3     best_sum = 0  # yoki: float ('- inf')4     joriy_sum = 05     uchun x yilda raqamlar:6         joriy_sum = maksimal(0, joriy_sum + x)7         best_sum = maksimal(best_sum, joriy_sum)8     qaytish best_sum

Algoritmning ushbu versiyasi 0 qiymatini qaytaradi, agar kiritishda ijobiy elementlar bo'lmasa (shu jumladan kirish bo'sh bo'lsa). Bo'sh ichki jadvallarni taqiqlaydigan muammoning varianti uchun, best_sum o'rniga salbiy cheksizlikka boshlash kerak^[11] va shuningdek for for loopida joriy_sum sifatida yangilanishi kerak maksimal (x, joriy_sum + x).^[7-eslatma]Bunday holda, agar kirishda ijobiy element bo'lmasa, qaytarilgan qiymat eng katta element (ya'ni eng kam salbiy qiymat) qiymatiga yoki agar kirish bo'sh bo'lsa, salbiy cheksizlikka teng bo'ladi.

Algoritmni maksimal subarrayning boshlanish va tugash ko'rsatkichlarini kuzatib borish uchun o'zgartirish mumkin:

 1 def max_subarray(raqamlar): 2     "" "Eng katta yig'indisi bo'lgan qo'shni subarrayni toping." "" 3     best_sum = 0  # yoki: float ('- inf') 4     best_start = best_end = 0  # yoki: yo'q 5     joriy_sum = 0 6     uchun joriy_end, x yilda sanab o'tish(raqamlar): 7         agar joriy_sum <= 0: 8             # Joriy elementda yangi ketma-ketlikni boshlang 9             joriy_ boshlanish = joriy_end10             joriy_sum = x11         boshqa:12             # Mavjud ketma-ketlikni joriy element bilan kengaytiring13             joriy_sum += x14 15         agar joriy_sum > best_sum:16             best_sum = joriy_sum17             best_start = joriy_ boshlanish18             best_end = joriy_end + 1  # the +1 - "best_end" ni eksklyuziv qilish19 20     qaytish best_sum, best_start, best_end

Python-da massivlar 0 dan boshlab indekslanadi va end indeks odatda chiqarib tashlanadi, shuning uchun [-11, 22, 33, -44] qatoridagi subarray [22, 33] 1 indeksdan boshlanib, indeksdan tugaydi. 3.

Ushbu algoritm maqbul pastki tuzilmalardan foydalanganligi sababli (har bir pozitsiyada tugaydigan maksimal subarray oddiy, shunga o'xshash, lekin kichikroq va bir-birining ustiga chiqadigan subproblemdan hisoblab chiqiladi: oldingi pozitsiyada tugaydigan maksimal subarray) bu algoritmni oddiy / ning ahamiyatsiz misoli dinamik dasturlash.

Kadane algoritmining ishlash vaqti murakkabligi ${displaystyle O (n)}$ .^[4]^[7]

Umumlashtirish

Shu kabi muammolar yuqori o'lchovli massivlar uchun ham tug'ilishi mumkin, ammo ularning echimlari ancha murakkab; qarang, masalan, Takaoka (2002). Brodal va Yorgensen (2007) topishni ko'rsatdi k eng kichik subarray yig'indilari bir o'lchovli massivda, optimal vaqt chegarasida ${displaystyle O (n + k)}$ .

Maksimal sum k-biriktirilgan subarraylarni optimal vaqt chegarasida ham hisoblash mumkin ${displaystyle O (n + k)}$ .^[12]

Shuningdek qarang

Jami summa muammosi

Izohlar

^ Umumiy yig'indilarning oldindan hisoblangan jadvalidan foydalanish orqali ${displaystyle S [k] = sum _ {x = 1} ^ {k} A [x]}$ subarray summasini hisoblash uchun ${displaystyle sum _ {x = i} ^ {j} A [x] = S [j] -S [i-1]}$ doimiy vaqt ichida
^ chunki har bir algoritm hech bo'lmaganda bir marta massivni bir marta skanerlashi kerak O(n) vaqt
^ nomlangan MaxEndingHere yilda Bentli (1989) va v yilda Gris (1982)
^ nomlangan MaxSoFar yilda Bentli (1989) va s yilda Gris (1982)
^ Ushbu summa ${displaystyle 0}$ qachon ${displaystyle i = j}$ , bo'sh subarrayga mos keladi ${displaystyle A [jldots j-1]}$ .
^ Python kodida, ${displaystyle A [j]}$ sifatida ifodalanadi x, indeks bilan ${displaystyle j}$ chap yopiq.
^ Oxirgi modifikatsiya tomonidan eslatilmagan bo'lsa-da Bentli (1989), o'zgartirilgan tsiklning o'zgarmasligini ta'minlashga erishadi joriy_sum ${displaystyle = max _ {iin {1, ..., j}} A [i] + ... + A [j]}$ boshida ${displaystyle j}$ th qadam.

Adabiyotlar

^ Bentli 1989 yil, p. 69.
^ Bentli 1989 yil, p. 70.
^ Bentli 1989 yil, p. 73.
^ ^a ^b ^v Bentli 1989 yil, p. 74.
^ ^a ^b Bentli 1984 yil, p. 868-869.
^ Bentli 1989 yil, p. 76-77.
^ ^a ^b ^v Gries 1982 yil, p. 211.
^ Gries 1982 yil, p. 209-211.
^ Qush 1989 yil, 8-bo'lim, 126-bet.
^ Backurs, Dikkala & Tzamos 2016.
^ Bentli 1989 yil, p. 78,171.
^ Bengtsson va Chen 2007 yil.

Backurs, Arturs; Dikkala, Nishant; Tzamos, Christos (2016), "Maksimal og'irlik to'rtburchaklar uchun qattiq qattiqlik natijalari", Proc. 43-Xalqaro avtomatika, tillar va dasturlash bo'yicha kollokvium: 81:1–81:13, doi:10.4230 / LIPIcs.ICALP.2016.81, S2CID 12720136
Bae, Sung Yun (2007), Umumlashtirilgan maksimal subarray masalasi uchun ketma-ket va parallel algoritmlar (PDF) (Doktorlik dissertatsiyasi), Kenterbury universiteti, S2CID 2681670.
Bengtsson, Fredrik; Chen, Jingsen (2007), Maksimal balli segmentlarni hisoblash (PDF) (Tadqiqot hisoboti), Luleå Texnologiya Universiteti
Bentli, Jon (1984), "Marvaridlarni dasturlash: algoritmni loyihalash usullari", ACM aloqalari, 27 (9): 865–873, doi:10.1145/358234.381162, S2CID 207565329
Bentli, Jon (may 1989), Marvaridlarni dasturlash (2-nashr?), Reading, MA: Addison Uesli, ISBN 0-201-10331-1
Qush, Richard S. (1989), "Dasturni hisoblash uchun algebraik identifikatorlar" (PDF), Kompyuter jurnali, 32 (2): 122–126, doi:10.1093 / comjnl / 32.2.122
Brodal, Gert Stolting; Yorgensen, Allan Grönlund (2007), "uchun chiziqli vaqt algoritmi k maksimal summa muammosi ", Kompyuter fanining matematik asoslari, Kompyuter fanidan ma'ruza matnlari, 4708, Springer-Verlag, 442-453 betlar, doi:10.1007/978-3-540-74456-6_40.
Gris, Devid (1982), "Loop invariants va looplarini ishlab chiqish bo'yicha standart strategiya to'g'risida eslatma" (PDF), Kompyuter dasturlash fanlari, 2 (3): 207–241, doi:10.1016/0167-6423(83)90015-1, hdl:1813/6370
Takaoka, Tadao (2002), "Masofaviy matritsani ko'paytirish bo'yicha subarray maksimal muammosi uchun samarali algoritmlar", Nazariy kompyuter fanidagi elektron yozuvlar, 61: 191–200, doi:10.1016 / S1571-0661 (04) 00313-5.
Tamaki, Xisao; Tokuyama, Takeshi (1998), "Matritsani ko'paytirishga asoslangan subarray maksimal muammo algoritmlari", Diskret algoritmlar bo'yicha 9-simpozium (SODA) materiallari.: 446–452, olingan 17-noyabr, 2018

Tashqi havolalar

TAN, Lirong. "Subarray yig'indisining maksimal muammolari" (PDF). Arxivlandi asl nusxasi (PDF) 2015-10-10 kunlari. Olingan 2017-10-26.
Mu, Shin-Cheng (2010). "Maksimal segmentlar yig'indisi muammosi: kelib chiqishi va kelib chiqishi".
"Subarrayning maksimal muammosi to'g'risida eslatmalar". 2012.
www.algorithmist.com
alexeigor.wikidot.com
Rosetta kodidagi keyingi eng katta summa muammosi
geeksforgeeks sahifasi Kadane algoritmida

[6] Umumiy yig'indilarning oldindan hisoblangan jadvalidan foydalanish orqali ${displaystyle S [k] = sum _ {x = 1} ^ {k} A [x]}$ subarray summasini hisoblash uchun ${displaystyle sum _ {x = i} ^ {j} A [x] = S [j] -S [i-1]}$ doimiy vaqt ichida

[9] unki har bir algoritm hech bo'lmaganda bir marta massivni bir marta skanerlashi kerak O(n) vaqt

[13] MaxEndingHere yilda Bentli (1989) va v yilda Gris (1982)

[14] MaxSoFar yilda Bentli (1989) va s yilda Gris (1982)

[15] Ushbu summa ${displaystyle 0}$ qachon ${displaystyle i = j}$ , bo'sh subarrayga mos keladi ${displaystyle A [jldots j-1]}$ .

[16] Python kodida, ${displaystyle A [j]}$ sifatida ifodalanadi x, indeks bilan ${displaystyle j}$ chap yopiq.

[18] Oxirgi modifikatsiya tomonidan eslatilmagan bo'lsa-da Bentli (1989), o'zgartirilgan tsiklning o'zgarmasligini ta'minlashga erishadi joriy_sum ${displaystyle = max _ {iin {1, ..., j}} A [i] + ... + A [j]}$ boshida ${displaystyle j}$ th qadam.

[FOOTNOTEBentley198969-1] Bentli 1989 yil, p. 69.

[FOOTNOTEBentley198970-2] Bentli 1989 yil, p. 70.

[FOOTNOTEBentley198973-3] Bentli 1989 yil, p. 73.

[FOOTNOTEBentley198974-4] v Bentli 1989 yil, p. 74.

[FOOTNOTEBentley1984868-869-5] Bentli 1984 yil, p. 868-869.

[FOOTNOTEBentley198976-77-7] Bentli 1989 yil, p. 76-77.

[FOOTNOTEGries1982211-8] v Gries 1982 yil, p. 211.

[FOOTNOTEGries1982209-211-10] Gries 1982 yil, p. 209-211.

[FOOTNOTEBird1989Sect.8,_p.126-11] Qush 1989 yil, 8-bo'lim, 126-bet.

[FOOTNOTEBackursDikkalaTzamos2016-12] Backurs, Dikkala & Tzamos 2016.

[FOOTNOTEBentley198978,171-17] Bentli 1989 yil, p. 78,171.

[FOOTNOTEBengtssonChen2007-19] Bengtsson va Chen 2007 yil.

[1]

[2]

[3]

[4]

[5]

[1-eslatma]

[6]

[7]

[2-eslatma]

[8]

[9]

[10]

[3-eslatma]

[4-eslatma]

[5-eslatma]

[6-eslatma]

[11]

[7-eslatma]

[12]