Darz ketadigan minimal daraxt - Minimum bottleneck spanning tree

Matematikada a darz ketgan minimal daraxt (MBST) yo'naltirilmagan grafikada a yoyilgan daraxt unda eng qimmat chekka iloji boricha arzonroq. Daraxt chekkasi - bu daraxtning eng yuqori tortilgan qirrasi. Agar grafada darcha chekkasining og'irligi kichikroq bo'lgan daraxt bo'lmasa, daraxt daraxti minimal darzlik daraxtidir.^[1] Yo'naltirilgan grafik uchun shunga o'xshash muammo quyidagicha tanilgan Shishani kamaytirish uchun eng kam daraxtzor (MBSA).

Ta'riflar

Yo'naltirilmagan grafikalar

Daraxt daraxti minimal

{ displaystyle G (V, E)}

Yo'naltirilmagan grafikada $G (V, E)$ va funktsiya $w : E \to R$ , ruxsat bering $S$ barcha daraxtlarning to'plami bo'ling T_men. Ruxsat bering B(T_men) har qanday daraxt daraxti uchun maksimal og'irlik chegarasi bo'lishi kerak T_men. Darz ketadigan minimal daraxtlar to'plamini aniqlaymiz S′ Har bir kishi uchun $T j \in S'$ va $T k \in S$ bizda ... bor $B (T j) \leq B (T k)$ Barcha uchun men vak.^[2]

O'ngdagi grafik MBSTga misol bo'lib, grafadagi qizil qirralarning MBST ning hosil bo'ladi $G (V, E)$ .

Yo'naltirilgan grafikalar

Shishani eng kam o'sadigan daraxtzor G (V, E)

Grafik arborescence G ning yo'naltirilgan daraxti G belgilangan tugundan yo'naltirilgan yo'lni o'z ichiga oladi L kichik to'plamning har bir tuguniga V′ Ning $V \{L}$ . Tugun L daraxtzorlikning ildizi deyiladi. Arborescence, agar bo'lsa, keng tarqalgan daraxtzorlikdir $V′ = V \{L}$ . MBST bu holda eng kam to'siq chekkasiga ega bo'lgan keng tarqalgan daraxtzor hisoblanadi. MBST bu holda Minimal Bottleneck Spanning Arborescence (MBSA) deb nomlanadi.

O'ngdagi grafik MBSA ga misol bo'lib, qizil qirralarning MBSA ning shaklini tashkil etadi $G (V, E)$ .

Xususiyatlari

MST (yoki.) minimal daraxt daraxti ) albatta MBST, ammo MBST albatta MST emas.^[3]

^[4]

Kamerinining yo'naltirilmagan grafikalar algoritmi

Kamerini taklif qildi^[5] an algoritm yo'naltirilmagan, bog'langan holda minimal darzlik daraxtini (MBST) olish uchun foydalaniladi, chekka o'lchovli grafik 1978 yilda. Bu yarmi qirralarni ikkita to'plamga ajratadi. Bir to'plamdagi qirralarning og'irligi ikkinchisidan ko'p emas. Agar a yoyilgan daraxt faqat kichik qirralarning chekkalari bilan o'rnatilgan subgrafada mavjud bo'lib, u subgrafda MBSTni hisoblab chiqadi, subgrafning MBSTi asl grafikaning MBSTiga to'g'ri keladi. Agar a yoyilgan daraxt mavjud emas, u har bir ajratilgan komponentni yangi super cho'qqiga birlashtiradi, so'ngra MBSTni ushbu super cho'qqilar va qirralarning katta qirralarida hosil bo'lgan grafikada hisoblaydi. O'chirilgan har bir komponentdagi o'rmon asl grafikadagi MBST qismidir. Grafada ikkita (super) tepaliklar qolguncha va ularning orasiga eng kichik og'irlikdagi bitta chekka qo'shilguncha ushbu amalni takrorlang. MBST oldingi bosqichlarda topilgan barcha qirralardan tashkil topgan.^[4]

Psevdokod

Protsedurada ikkita kirish parametrlari mavjud. G bu grafik, w grafadagi barcha qirralarning vazn massividir G.^[6]

 1  funktsiya MBST (grafik G, og'irliklar w) 2  E ← qirralarning to'plami G  3  agar | E | = 1 keyin qaytish E boshqa 4      A ← yarim qirralar E uning og'irliklari o'rtacha 5 vaznidan kam emas B ← E - A 6      F ← o'rmon G_B 7      agar F bir daraxt keyin 8          qaytish MBST (G_B,w) 9      boshqa 10         qaytish MBST ((G_A)_η, w)  ${ displaystyle cup}$  F

Yuqorida (G_A)_η super cho'qqilar (ajratilgan komponentdagi cho'qqilarni bitta deb hisoblash bilan) va qirralardan tashkil topgan subgrafdir. A.

Ish vaqti

Algoritm ishlamoqda O (E) vaqt, qaerda E qirralarning soni. Ushbu chegaraga quyidagicha erishiladi:

medianing algoritmlari bilan ikkita to'plamga bo'lish O(E)
ichida o'rmon topish O(E)
har bir takrorlashda E dagi yarim qirralarni hisobga olgan holda O(E + E/2 + E/4 + ··· + 1) = O(E)

Misol

Quyidagi misolda MBST hosil qilish uchun yashil qirralardan foydalanilgan va qizil chiziqlar algoritm bosqichlari davomida hosil bo'lgan yuqori tepaliklarni bildiradi.

	Algoritm og'irliklarga nisbatan qirralarni ikki to'plamga ajratadi. Yashil qirralar - og'irliklari iloji boricha kichikroq bo'lgan qirralar.
	Subgrafda faqat kichik qirralarning chekkalari o'rnatilib shakllangan daraxt mavjud. Ushbu subgrafada MBST topishni takrorlang.
	Hozirgi subgrafada biron bir daraxt mavjud bo'lmaganligi sababli, hozirgi kichik qirralarning chekkalari o'rnatilgan. O'chirilgan komponentning tepalarini super cho'qqiga (chiziqli qizil maydon bilan belgilanadi) birlashtiring va so'ngra subgrafda katta cho'plar to'plamida super cho'qqilar va qirralar bilan hosil qilingan MBSTni toping. Har bir ajratilgan komponent ichida hosil bo'lgan o'rmon asl grafadagi MBST tarkibiga kiradi.
	Ko'proq tepaliklarni super cho'qqiga birlashtirib, shunga o'xshash amallarni takrorlang.
	Algoritm algoritm davomida topilgan qirralarning yordamida MBST ni oladi.

Yo'naltirilgan grafikalar uchun MBSA algoritmlari

Yo'naltirilgan grafika uchun ikkita algoritm mavjud: Kamerinining MBSA va boshqasini Gabov va Tarjandan topish algoritmi.^[4]

Kamerinining MBSA uchun algoritmi

Yo'naltirilgan grafika uchun Camerini algoritmi MBSA ning tirbandlik qiymati sifatida maksimal narxga ega bo'lgan qirralarning to'plamini topishga qaratilgan. Bu qirralarning to'plamini ajratish orqali amalga oshiriladi E ikkita to'plamga A va B va to'plamni saqlash T bu ma'lum bo'lgan to'plam G_T ko'payib borayotgan daraxtzorga ega emas, ko'paymoqda T tomonidan B har doim maksimal daraxtzorligi G(B ∪ T) ning keng tarqalgan daraxtzorligi emas G, aks holda biz kamayamiz E tomonidanA. Vaqtning umumiy murakkabligi O(E jurnalE).^[5]^[4]

Psevdokod

funktsiya MBSA (G, w, T) bu    E ← qirralarning to'plami G     agar | E - T | > 1 keyin        A ← UH (E-T) B ← (E - T) − A        F ← Bush (G_AMMA)        agar F G ning keng tarqalgan daraxtzorligi hisoblanadi keyin            S ← F MBSA ((G_AMMA), w, T)        boshqa            MBSA (G, w, TUB);

T E ning kichik qismini aks ettiradi, ular uchun G ma'lum_T "a" tugunida ildiz otgan biron bir daraxtzorni o'z ichiga olmaydi. Dastlab T bo'sh
UH G (E-T) qirralarning to'plamini oladi va A ⊂ (E-T) ni quyidagicha qaytaradi:
1. ${ displaystyle | A | = left lfloor { frac {(| E-T |)} {2}} right rfloor}$
2. V_a ≥ V_b , a ∈ A va b ∈ B uchun
BUSH (G) "a" tugunida ildiz otgan G ning maksimal daraxtzorligini qaytaradi
Yakuniy natija S bo'ladi

Misol

	Ushbu algoritmning birinchi takrorlanishidan so'ng biz quyidagini olamiz $F$ va $F$ ning keng tarqalgan daraxtzorligi emas $G$ , Shunday qilib biz kodni ishga tushiramiz ${ displaystyle MBSA (G, w, T stakan B).}$
	Ikkinchi takrorlashda biz ${ displaystyle F '}$ va ${ displaystyle F '}$ shuningdek, keng tarqalgan daraxtzor emas $G$ , Shunday qilib biz kodni ishga tushiramiz ${ displaystyle MBSA (G, w, T ' cup B')}$
	Uchinchi takrorlashda biz ${ displaystyle F ''}$ va ${ displaystyle F ''}$ ning keng tarqalgan daraxtzorligi hisoblanadi $G$ , Shunday qilib biz kodni ishga tushiramiz ${ displaystyle MBSA (G_ {T '' cup B ''}, w, T '')}$
	biz ishlayotganimizda ${ displaystyle MBSA (G_ {T '' cup B ''}, w, T '')}$ , ${ displaystyle \| E-T \|}$ 1 ga teng, bu 1 dan katta emas, shuning uchun algoritm qaytadi va yakuniy natija bo'ladi ${ displaystyle S = F "'}$ .

MBSA uchun Gabow va Tarjan algoritmi

Gabow va Tarjan modifikatsiyasini taqdim etdi Dijkstra algoritmi MBSA ishlab chiqaradigan bir manbali eng qisqa yo'l uchun. Ularning algoritmi ishlaydi O(E + V jurnalV) vaqt Fibonachchi uyumi ishlatilgan.^[7]

Psevdokod

 Grafik uchun G (V, E), F - bu vertikalar to'plamidir V. Dastlab, F = {s} qayerda s grafaning boshlang'ich nuqtasidir G va v(s) = -∞ 1  funktsiya MBSA-GT (G, w, T) 2      takrorlang | V | marta 3 tanlang v minimal bilan v(v) dan F; 4 uni o'chirib tashlang F; 5          uchun ∀ chekka (v, w) qil 6              agar w ∉ F yoki ∉ daraxt keyin 7 qo'shish w ga F;           8                  v(w) = v(v, w); 9                  p(w) = v;      10             boshqa 11                 agar w ∈ F va c (w)> c (v, w) keyin 12                     v(w) = v(v, w); 13                     p(w) = v;

Misol

Quyidagi misol algoritm qanday ishlashini ko'rsatadi.

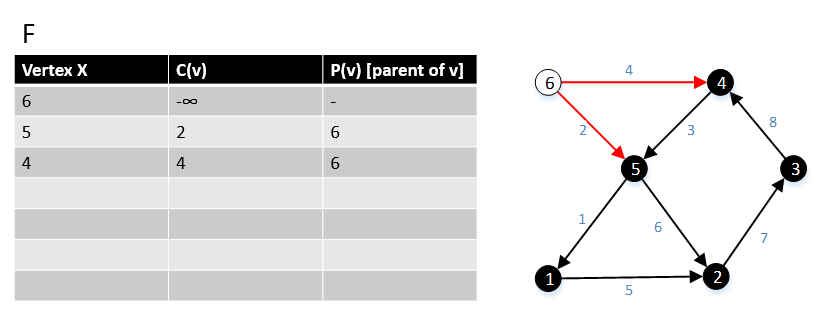Algoritmning birinchi bosqichida biz G grafikadan s ildizini tanlaymiz, yuqoridagi rasmda 6 vertex s ildiz hisoblanadi. Keyin biz barcha chekkalarni (6, w) ∈ E va ularning narxini c (6, w) topdik, bu erda w ∈ V.

Keyin biz G grafasidagi 5-chi cho'qqiga o'tamiz, biz barcha chekkalarni (5, w) ∈ E va ularning qiymati c (5, w) ni topdik, bu erda w ∈ V.

Keyin G grafikadagi vertikal 4 ga o'tamiz, hamma qirrasini (4, w) ∈ E va ularning narxini c (4, w) topdik, bu erda w ∈ V. Biz bu chekka (4,5)> chekka (6.5), shuning uchun biz chekkani (6,5) ushlab turamiz va qirrani (4,5) olib tashlaymiz.

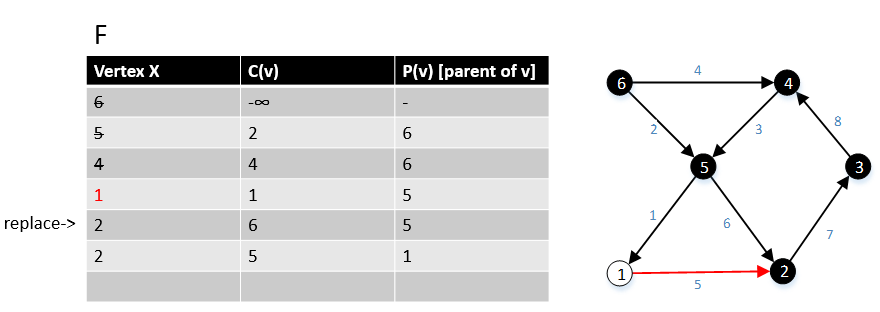Keyin G grafasidagi 1 tepasiga o'tamiz, barcha (1, w) ∈ E qirralarni va ularning narxini c (1, w) topdik, bu erda w ∈ V. Biz bu chekka (5,2)> chekka (1,2), shuning uchun biz chekkani (5,2) olib tashlaymiz va (1,2) chetini ushlab turamiz.

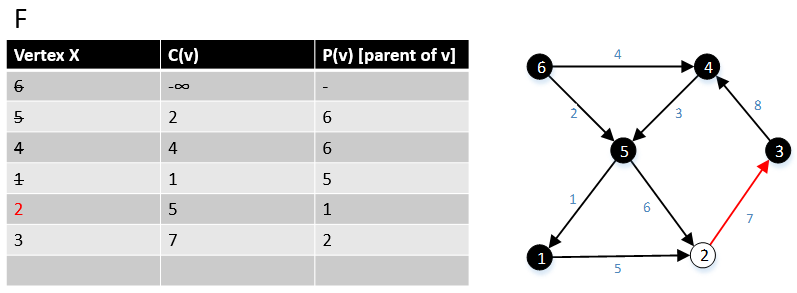Keyin biz G grafasidagi 2-vertikalga o'tamiz, biz barcha chekkalarni (2, w) ∈ E va ularning qiymati c (2, w) ni topdik, bu erda w ∈ V.

Keyin biz G grafasidagi 3-chi cho'qqiga o'tamiz, barcha (3, w) ∈ E va ularning narxlarini c (3, w) topdik, bu erda w ∈ V. Biz (3,4)> chekka (6,4), shuning uchun biz chekkani (3,4) olib tashlaymiz va chekkani (6,4) saqlaymiz.

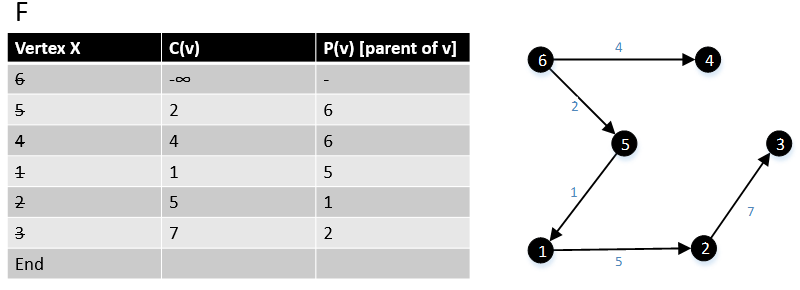G grafasidagi barcha tepaliklarni aylanib o'tgandan so'ng, algoritm tugadi.

Tarjan va Gabov tomonidan taklif qilingan yana bir yondashuv $O (E jurnal * V)$ bu Kamerinining MBSA algoritmiga juda o'xshash bo'lgan, ammo qirralarning to'plamini har bir iteratsiya uchun ikkita to'plamga bo'lishdan ko'ra, kamdan-kam grafikalar uchun, $K (men)$ unda kiritilgan men sodir bo'lgan bo'linishlar soni yoki boshqacha aytganda takrorlanish soni va $K (men)$ - har bir takrorlash uchun bo'linishi kerak bo'lgan bo'linadigan to'plamlar sonini bildiruvchi ortib boruvchi funktsiya. $K (men) = 2 k (men - 1)$ bilan $k (1) = 2$ . Algoritm topadi $λ *$ bunda u har qanday MBSA-da darz ketgan tomonning qiymati hisoblanadi. Keyin $λ *$ ichida har qanday arborescence mavjud $G (λ *)$ unda MBSA mavjud $G (λ *)$ uning barcha xarajatlari bo'lgan grafik $\leq λ *$ .^[4]^[7]

Adabiyotlar

^ Daraxt daraxti haqida hamma narsa
^ Murali, T. M. (2009), Minimal uzunlikdagi daraxtlarning qo'llanilishi (PDF)
^ 3-savolda ushbu da'vo uchun sizning dalilingiz bor (PDF)
^ ^a ^b ^v ^d ^e Traboulsi, Ahmad (2014), Daraxtlar (PDF), dan arxivlangan asl nusxasi (PDF) 2016-03-04 da, olingan 2014-12-28
^ ^a ^b Kamerini, PM (1978), "Min-max uzunlikdagi daraxtlar muammosi va ba'zi kengaytmalar", Axborotni qayta ishlash xatlari, 7 (1): 10, doi:10.1016/0020-0190(78)90030-3
^ Cui, Yuxiang (2013), Shishani eng kam qoplaydigan daraxt (PDF), dan arxivlangan asl nusxasi (PDF) 2016-03-04 da, olingan 2014-12-28
^ ^a ^b Gabov, Garold N; Tarjan, Robert E (1988). "Ikki to'siqni optimallashtirish muammolari algoritmlari". Algoritmlar jurnali. 9 (3): 411–417. doi:10.1016/0196-6774(88)90031-4. ISSN 0196-6774.

[1] Daraxt daraxti haqida hamma narsa

[2] Murali, T. M. (2009), Minimal uzunlikdagi daraxtlarning qo'llanilishi (PDF)

[3] 3-savolda ushbu da'vo uchun sizning dalilingiz bor (PDF)

[Traboulsi2014-4] v ^d ^e Traboulsi, Ahmad (2014), Daraxtlar (PDF), dan arxivlangan asl nusxasi (PDF) 2016-03-04 da, olingan 2014-12-28

[Camerini1978-5] Kamerini, PM (1978), "Min-max uzunlikdagi daraxtlar muammosi va ba'zi kengaytmalar", Axborotni qayta ishlash xatlari, 7 (1): 10, doi:10.1016/0020-0190(78)90030-3

[6] Cui, Yuxiang (2013), Shishani eng kam qoplaydigan daraxt (PDF), dan arxivlangan asl nusxasi (PDF) 2016-03-04 da, olingan 2014-12-28

[GabowTarjan1988-7] Gabov, Garold N; Tarjan, Robert E (1988). "Ikki to'siqni optimallashtirish muammolari algoritmlari". Algoritmlar jurnali. 9 (3): 411–417. doi:10.1016/0196-6774(88)90031-4. ISSN 0196-6774.

[1]

[2]

[3]

[4]

[5]

[6]

[7]