Simson chizig'i - Simson line

Yilda geometriya berilgan uchburchak ABC va a nuqta P uning ustida aylana, eng yaqin uchta nuqta P chiziqlarda AB, ACva Miloddan avvalgi bor kollinear.[1] Ushbu nuqtalar orasidagi chiziq Simson chizig'i ning Puchun nomlangan Robert Simson.[2] Kontseptsiya birinchi marta nashr etilgan, ammo Uilyam Uolles 1799 yilda.[3]
The suhbatlashish bu ham to'g'ri; agar uchta eng yaqin nuqta P uchta satrda chiziqli va ikkita satr parallel bo'lmaydi, keyin P uchta chiziq hosil qilgan uchburchakning aylanasida yotadi. Yoki boshqacha qilib aytganda, uchburchakning Simson chizig'i ABC va nuqta P faqat pedal uchburchagi ning ABC va P Bu to'g'ri chiziqqa degeneratsiya qilingan va bu holat cheklovlarni cheklaydi lokus ning P uchburchakning aylanasini kuzatib borish ABC.
Tenglama
Uchburchakni kompleks tekislikka joylashtirib, ABC uchburchakni birlik bilan bo'lsin aylana joylashgan joylari murakkab koordinatalarga ega bo'lgan tepaliklarga ega a, b, v, va murakkab koordinatalari bilan P ga ruxsat bering p aylana atrofida nuqta bo'ling. Simson chizig'i nuqta to'plamidir z qoniqarli[4]:Taklif 4
bu erda ustki panel ko'rsatiladi murakkab konjugatsiya.
Xususiyatlari
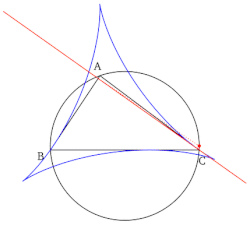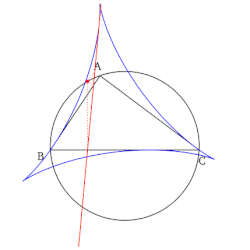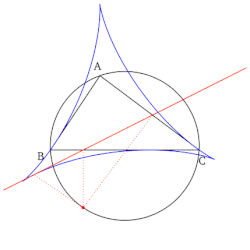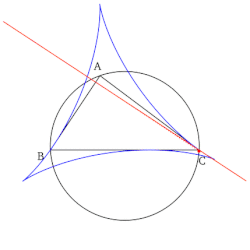
- Uchburchak tepaligining Simson chizig'i bu balandlik uchburchagi shu tepadan tushgan va nuqta Simson chizig'i bir-biriga qarama-qarshi tepaga - uchburchakning o'sha tepaga qarama-qarshi tomoni.
- Agar P va Q aylana doirasidagi nuqtalar, keyin Simson chiziqlari orasidagi burchak P va Q yoyning yarim burchagi PQ. Xususan, agar nuqtalar bir-biriga qarama-qarshi bo'lsa, ularning Simson chiziqlari perpendikulyar va bu holda chiziqlarning kesishishi to'qqiz nuqta doirasi.
- Ruxsat berish H ni belgilang ortsentr uchburchakning ABC, Simson liniyasi P segmentni ikkiga ajratadi PH to'qqiz nuqta doirada yotadigan nuqtada.
- Bir xil aylana bilan ikkita uchburchak berilgan, nuqta Simson chiziqlari orasidagi burchak P ikkala uchburchak uchun aylanaga bog'liq emas P.
- Barcha Simson chiziqlari to'plami chizilganida an hosil bo'ladi konvert deb nomlanuvchi delta shaklida Shtayner deltasi mos yozuvlar uchburchagi.
- Simson chizig'ining mos yozuvlar uchburchagi tomoniga to'g'ri kelishi (yuqoridagi birinchi xususiyatga qarang) ushbu yon chiziqda noan'anaviy nuqta hosil qiladi. Bu nuqta balandlik oyoqining (yon chiziqqa tushirilgan) yon chiziq chizig'ining o'rta nuqtasiga nisbatan aks etishi. Bundan tashqari, bu nuqta mos yozuvlar uchburchagi tomoni va uning Shtayner deltasi orasidagi teginuvchi nuqtadir.
- Parallelogramma bo'lmagan to'rtburchakda Simson nuqtasi deb nomlangan bitta va faqat bitta pedal nuqtasi mavjud bo'lib, unga nisbatan to'rtburchakdagi oyoqlar kollinear bo'ladi.[5] Trapetsiyaning Simson nuqtasi ikkita parallel bo'lmagan tomonlarning kesishish nuqtasidir.[6]:p. 186
- Kamida 5 tomoni bo'lgan hech qanday qavariq ko'pburchakda Simson chizig'i mavjud emas.[7]
Mavjudlikning isboti
Isbotlash usuli shuni ko'rsatishdir . tsiklik to'rtburchak, shuning uchun . tsiklik to'rtburchak (Fales teoremasi ), shuning uchun . Shuning uchun . Endi tsiklikdir, shuning uchun . Shuning uchun .
Muqobil dalil

Qo'shni rasmdagi Z nuqta qanday bo'lishidan qat'i nazar, a + c 90, shuningdek Z nuqta qanday bo'lishidan qat'iy nazar, c va b teng bo'ladi, shuning uchun bizda quyidagilar mavjud:
a + c = 90
∴ a + b = 90… (c va b teng) (1)
Endi, burchak o'lchovini ko'rib chiqing: a + 90 + b.
Agar bu burchak 180 ga teng ekanligini ko'rsatsak, unda Simpson teoremasi isbotlangan.
(1) dan bizda + 90 + b = 180 mavjud
Q.E.D.
Umumlashtirish
Umumlashtirish 1

- Ruxsat bering ABC uchburchak bo'ling, circum chiziq aylana aylanadan o'tsin Ova bir nuqtaga ruxsat bering P aylana atrofida yotish. Ruxsat bering AP, BP, CP meet da uchrashmoq Ap, Bp, Cp navbati bilan. Ruxsat bering A0, B0, C0 ning prognozlari bo'lishi Ap, Bp, Cp ustiga Miloddan avvalgi, CA, ABnavbati bilan. Keyin A0, B0, C0 kollinear. Bundan tashqari, yangi chiziq PH, qayerda H $ Delta $ ortosentridirABC. Agar ℓ o'tib ketsa P, chiziq Simson chizig'iga to'g'ri keladi. [8][9][10]

Umumlashtirish 2
- Uchburchakning tepalari bo'lsin ABC yotish konus Γ va ruxsat bering Q, P tekislikda ikki nuqta bo'lishi kerak. Ruxsat bering PA, PB, kompyuter konusni kesishadi A1, B1, C1 navbati bilan. QA1 kesishadi Miloddan avvalgi da A2, QB1 kesishadi AC da B2va QC1 kesishadi AB da C2. Keyin to'rtta nuqta A2, B2, C2va P agar shunday bo'lsa, kollinear bo'ladi Q konusning ustida yotadi Γ.[11]
Umumlashtirish 3
- R. F. Cyster teoremani ga umumlashtirdi tsiklik to'rtburchaklar yilda Tsiklik to'rtburchakning Simson chiziqlari
Shuningdek qarang
Adabiyotlar
- ^ H.S.M. Kokseter va S.L. Greitser, Geometriya qayta ko'rib chiqildi, Matematik. Dos. Amerika, 1967: s.41.
- ^ "Gibson tarixi 7 - Robert Simson". 2008-01-30.
- ^ http://www-groups.dcs.st-and.ac.uk/history/Biographies/Wallace.html
- ^ Todor Zaharinov, "Simson uchburchagi va uning xususiyatlari", Forum Geometricorum 17 (2017), 373--381. http://forumgeom.fau.edu/FG2017volume17/FG201736.pdf
- ^ Daniela Ferrarello, Mariya Flaviya Mammana va Mario Pennisi, "Pedalli ko'pburchaklar", Forum Geometricorum 13 (2013) 153–164: 4-teorema.
- ^ Olga Radko va Emmanuel Tsukerman, "Perpendikulyar bisektor qurilishi, izoptik nuqta va to'rtburchakning Simson chizig'i", Forum Geometricorum 12 (2012). [1]
- ^ Tsukerman, Emmanuel (2013). "Simson liniyasini parabolalarning alohida analoglari sifatida qabul qiladigan ko'pburchaklar to'g'risida" (PDF). Forum Geometricorum. 13: 197–208.
- ^ "Simson liniyasining umumlashtirilishi". Tugun. 2015 yil aprel.
- ^ Nguyen Van Lin (2016), "Daoning Simson liniyasi teoremasini umumlashtirganligining yana bir sintetik isboti" (PDF), Forum Geometricorum, 16: 57–61
- ^ Nguyen Le Phuoc va Nguyen Chuong Chi (2016). 100.24 Daoning Simson chiziq teoremasini umumlashtirishining sintetik isboti. Matematik gazeta, 100, 341-345 bet. doi: 10.1017 / mag.2016.77. Matematik gazeta
- ^ Smit, Geoff (2015), "99.20 Proektiv Simson liniyasi", Matematik gazeta, 99 (545): 339–341, doi:10.1017 / mag.2015.47
Tashqi havolalar
- Simson Line da tugun.org
- F. M. Jekson va Vayshteyn, Erik V. "Simson Line". MathWorld.
- Noyberg teoremasi va Simson-Uollas chizig'ining umumlashtirilishi da Dinamik geometriya eskizlari, interaktiv dinamik geometriya eskiz.










