Nishab maydoni - Slope field

Birinchi darajadagi echimlar differentsial tenglama[1] skalyar funktsiyani y (x) 2 o'lchovli bo'shliqda x gorizontal va y vertikal yo'nalishda chizish mumkin. Mumkin echimlar qattiq egri chiziqlar shaklida chizilgan y (x) funktsiyalardir. Ba'zan differentsial tenglamani echish juda noqulay analitik ravishda. Keyin funktsiya egri chiziqlarining teginishlarini chizish mumkin, masalan. muntazam panjara ustida. Tangenslar panjara nuqtalaridagi funktsiyalarga tegishlidir. Biroq, yo'nalish maydoni differentsial tenglamaning xaotik jihatlari haqida ancha agnostikdir.
Ta'rif
Standart ish
Nishab maydonini quyidagi turdagi differentsial tenglamalar uchun aniqlash mumkin
- ,
berilgan sifatida geometrik ravishda talqin qilinishi mumkin Nishab ning teginish uchun grafik differentsial tenglama echimining (integral egri chiziq ) har bir nuqtada (x, y) nuqta koordinatalari funktsiyasi sifatida.[2]
Uni ikkita haqiqiy o'zgaruvchining haqiqiy qiymatli funktsiyasini tuzishning ijodiy usuli sifatida ko'rish mumkin planar rasm sifatida. Xususan, berilgan juftlik uchun , komponentlar bilan vektor nuqtada chizilgan ustida - samolyot. Ba'zan, vektor fitna inson ko'zini yaxshiroq qidirish uchun normallashtirilgan. Juftliklar to'plami to'rtburchaklar panjara yasash odatda rasm uchun ishlatiladi.
An izoklin (bir xil nishabga ega bo'lgan qatorlar qatori) ko'pincha nishab maydonini to'ldirish uchun ishlatiladi. Shaklning tenglamasida , izoklin - bu chiziq - sozlash orqali olingan samolyot doimiyga teng.
Differentsial tenglamalar tizimining umumiy holati
Diferensial tenglamalar tizimi berilgan
Nishab maydoni - bu nishab belgilarining massivi fazaviy bo'shliq (tegishli o'zgaruvchilar soniga qarab o'lchamlarning istalgan sonida, masalan, birinchi tartibli chiziqli holatda ikkita ODE, o'ng tomonda ko'rinib turganidek). Har bir nishab belgisi bir nuqtada markazlashtirilgan va vektorga parallel
- .
Nishab belgilarining soni, joylashuvi va uzunligi o'zboshimchalik bilan bo'lishi mumkin. Joylar odatda shunday tanlanadi, shunda ballar bir xil panjara qiling. Yuqorida tavsiflangan standart holat ifodalaydi . Differentsial tenglamalar tizimlari uchun nishab maydonining umumiy holatini tasavvur qilish oson emas .
Umumiy dastur
Kompyuterlar yordamida murakkab qiyalik maydonlari tezda charchamasdan amalga oshiriladi va shuning uchun ularni yaqinda amaliy qo'llanilishi shunchaki aniq umumiy echim izlanishidan oldin qanday echim bo'lishi kerakligini anglash uchun ishlatishdir. Agar mavjud bo'lsa, albatta, kompyuterlar ham bittasini echishi mumkin.
Agar aniq umumiy echim bo'lmasa, kompyuterlar grafik echimlarni raqamli ravishda topish uchun nishab maydonlaridan foydalanishlari mumkin (hatto ko'rsatilmagan bo'lsa ham). Bunday odatlarning namunalari Eyler usuli, yoki yaxshiroq, the Runge-Kutta usullari.
Nishab maydonlarini chizish uchun dasturiy ta'minot
Turli xil dasturiy ta'minot to'plamlari nishab maydonlarini tuzishi mumkin.
Yo'nalish maydon kodi GNU oktavi /MATLAB
funn = @(x,y)y-x; % funktsiyasi f (x, y) = y-x[x,y]=meshgrid(-5:0.5:5); x va y uchun% intervallaryon bag'irlari=funn(x,y); Nishab qiymatlarining% matritsasidy=yon bag'irlari./kv(1+yon bag'irlari.^2); % chiziq elementini normallashtiradi ...dx=bittasi(uzunlik(dy))./kv(1+yon bag'irlari.^2); dy ... va dx uchun% ... kattaliklarh=titroq(x,y,dx,dy,0.5); % yo'nalish maydonini chizisho'rnatilgan (h, "maxheadsize", 0.1); % bosh hajmini o'zgartirishUchun namunaviy kod Maksima
/ * y '= xy uchun maydon (integral egri chiziq olish uchun nuqtani bosing) * / plotdf (x * y, [x, -2,2], [y, -2,2]);
Uchun namunaviy kod Matematik
(* y '= xy * uchun maydon)VectorPlot[{1,x*y},{x,-2,2},{y,-2,2}]Uchun namunaviy kod SageMath[3]
var ('x, y') plot_slope_field (x * y, (x, -2,2), (y, -2,2))Misollar
- y '= x / y

Nishab maydoni

Integral egri chiziqlar
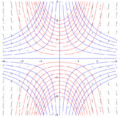
Izoklinalar (ko'k), nishab maydoni (qora) va ba'zi eritma egri chiziqlari (qizil)
Shuningdek qarang
- Differentsial tenglamalar misollari
- Vektorli maydon
- Differentsial tenglamalarga tatbiq etilgan laplas konvertatsiyasi
- Dinamik tizimlar va differentsial tenglamalar mavzulari ro'yxati
- Diferensial tenglamalarning sifat nazariyasi
Adabiyotlar
- ^ Vladimir A. Dobrushkin (2014). Amaliy differentsial tenglamalar: boshlang'ich kurs. CRC Press. p. 13. ISBN 978-1-4987-2835-5.
- ^ Andrey D. Polyanin; Aleksandr V. Manjirov (2006). Muhandislar va olimlar uchun matematikadan qo'llanma. CRC Press. p. 453. ISBN 978-1-58488-502-3.
- ^ https://doc.sagemath.org/html/en/reference/plotting/sage/plot/plot_field.html
- Blanshard, Pol; Devani, Robert L.; va Hall, Glen R. (2002). Differentsial tenglamalar (2-nashr). Bruks / Koul: Tompsonni o'rganish. ISBN 0-534-38514-1




![[1, f (x, y)]](https://wikimedia.org/api/rest_v1/media/math/render/svg/47b0f1a2b509928c2c7981d32549930250732a24)










