G'ildiraklarni faktorizatsiya qilish - Wheel factorization

Ushbu maqola mumkin talab qilish tozalamoq Vikipediya bilan tanishish uchun sifat standartlari. Muayyan muammo: Kompyuterni amalga oshirish algoritmi, psevdokod, keyingi ishlash tahlili va hisoblashning murakkabligi to'liq emas Iltimos yordam bering ushbu maqolani yaxshilang Agar imkoningiz bo'lsa. (2015 yil fevral) (Ushbu shablon xabarini qanday va qachon olib tashlashni bilib oling)

N = 2x3x5 = 30 bo'lgan g'ildirak faktorizatsiyasi. Sariq joylarda hech qanday asosiy narsa bo'lmaydi.

G'ildiraklarni faktorizatsiya qilish ning yaxshilanishi sinov bo'limi usuli tamsayı faktorizatsiyasi.

Sinovlarga bo'linish usuli bo'linuvchi topilguncha ketma-ket bo'linadigan sonni birinchi butun sonlarga (2, 3, 4, 5, ...) bo'lishdan iborat. G'ildirak faktorizatsiyasi uchun raqamlar kichik ro'yxatidan boshlanadi, deb nomlanadi asos - odatda birinchi bir nechta tub sonlar; keyin "." deb nomlangan ro'yxat hosil bo'ladi g'ildirakbo'lgan butun sonlarning koprime asosning barcha raqamlari bilan. Keyin songa bo'linadigan sonning eng kichik bo'linuvchisini topish uchun uni ketma-ket asosdagi va g'ildirakdagi sonlarga bo'linadi.

{2, 3} asosiga ko'ra, bu usul bo'linishlar sonini kamaytiradi 1/3 < 34% sinov bo'limi uchun zarur bo'lgan raqam. Kattaroq bazalar bu nisbatni yanada kamaytiradi; masalan, {2, 3, 5} to asoslari bilan 8/30 < 27%; va {2, 3, 5, 7} ga asoslanib 48/210 < 23%.

Odatiy misol

Birinchi bir necha tub sonlarning ({2, 3, 5}) asosidagi g'ildirakning "birinchi burilishi" quyidagilardan iborat:

7, 11, 13, 17, 19, 23, 29, 31.

Ikkinchi burilish 30, the qo'shib olinadi mahsulot birinchi navbatdagi raqamlarga asos. Uchinchi burilish, ikkinchi burilishga 30 ga qo'shilishi bilan olinadi va hokazo.

Usulni amalga oshirish uchun g'ildirakning ketma-ket ikkita elementi orasidagi o'sish, ya'ni

inc = [4, 2, 4, 2, 4, 6, 2, 6],

har bir burilishdan keyin bir xil bo'lib qoling.

Quyidagi taklif qilingan dastur yordamchi funktsiyadan foydalanadi div (n, k), yoki yo'qligini tekshiradigan n teng taqsimlanadi kva qaytadi to'g'ri Ushbu holatda, yolg'on aks holda. Ushbu dasturda faktorizatsiya qilinadigan raqam n, va dastur eng kichik bo'luvchini qaytaradi n.

test: = noto'g'riagar div (n, 2) = true keyin 2 qaytadi;agar div (n, 3) = true, keyin 3 qaytadi;agar div (n, 5) = true, keyin 5 ni qaytaradi;k := 7; men := 1esa test = noto'g'ri va k * k ≤ n qil    sinov: = div (n, k)    agar test = rost, keyin qaytish k    k := k + inc [men]    agar men < 8 keyin men := men + Yana 1 ta men := 1qaytish n

Butun sonning to'liq faktorizatsiyasini olish uchun hisoblash boshida g'ildirakni qayta ishga tushirmasdan davom ettirilishi mumkin. Bu to'liq faktorizatsiya uchun quyidagi dasturga olib keladi, bu erda "qo'shish" funktsiyasi ro'yxat bo'lishi kerak bo'lgan ikkinchi argument oxirida o'zining birinchi argumentini qo'shadi.

omillar: = [];esa div (n, 2) = true keyin omillar: = add (2, factor); n := n / 2;esa div (n, 3) = true keyin omillar: = add (3, factor); n := n / 3;esa div (n, 5) = true keyin omillar: = add (5, factor); n := n / 5;k := 7; men := 1esa k * k ≤ n qil    agar div (n, k) = rost keyin         qo'shish (k, omillar) n := n / k    boshqa        k := k + inc [men]        agar men < 8 keyin men := men + 1 boshqa men := 1qaytish qo'shish (n, omillar)

Boshqa taqdimot

G'ildirak faktorizatsiyasi asosan ro'yxatlarni yaratish uchun ishlatiladi tub sonlar oddiy matematik formuladan va birinchi tub sonlarning ancha kichik ro'yxatidan. Ushbu ro'yxatlar keyinchalik ishlatilishi mumkin sinov bo'limi yoki elaklar. Ushbu ro'yxatdagi barcha raqamlar asosiy emasligi sababli, bu samarasiz ortiqcha operatsiyalarni keltirib chiqaradi. Biroq, generatorlarning o'zi oddiy raqamlarning toza ro'yxatini saqlash bilan taqqoslaganda juda kam xotira talab qiladi. Boshlang'ich tub sonlarning kichik ro'yxati. Uchun to'liq parametrlarni tashkil etadi algoritm ro'yxatning qolgan qismini yaratish uchun. Ushbu generatorlar deb nomlanadi g'ildiraklar. Har bir g'ildirak raqamlarning cheksiz ro'yxatini yaratishi mumkin bo'lsa-da, ma'lum bir nuqtadan o'tib, raqamlar asosan oddiy bo'lishni to'xtatadi.

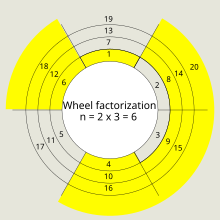
Usul keyinchalik rekursiv ravishda oddiy son sifatida qo'llanilishi mumkin g'ildirak elagi aniqroq g'ildiraklarni yaratish uchun. G'ildiraklarni faktorizatsiya qilish, g'ildiraklarni faktorizatsiyalash yordamida elaklarni va g'ildirak elaklarini ishlab chiqarish bo'yicha juda aniq ishlar Pol Pritchard tomonidan amalga oshirildi.^[1][2][3][4] bir qator turli algoritmlarni shakllantirishda. Faktorizatsiya g'ildiragidan foydalanishni tasavvur qilish uchun qo'shni diagrammada ko'rsatilganidek, tabiiy sonlarni doiralar atrofida yozishdan boshlash mumkin. Spikerlar soni shunchaki tanlanganki, asosiy sonlar spikerlarning ozchilik qismida to'planish tendentsiyasiga ega bo'ladi.

Namunaviy grafik protsedura

1. Faktorlashtiruvchi g'ildirakning asosini tashkil etadigan dastlabki bir necha tub sonlarni toping. Ular kichikroq faktorizatsiya g'ildiraklarining oldingi dasturlaridan ma'lum yoki ehtimol ularni yordamida topish orqali aniqlanadi Eratosfen elagi.
2. Natija berish uchun asosiy tub sonlarni birga ko'paytiring n bu faktorizatsiya g'ildiragining atrofi.
3. 1 dan raqamlarni yozing n doira ichida. Bu g'ildirakning bitta aylanishini ifodalovchi eng ichki doiradir.
4. 1 dan raqamlarga n ichki aylanada, 2-bosqichda qo'llanilgandek, birinchi darajadagi barcha asosiy sonlarni ko'paytiring. Ushbu kompozitsion sonni yo'q qilish, Eratosfen elagi kabi elak yordamida yoki kichikroq faktorizatsiya qo'llanilishi natijasida amalga oshiriladi. g'ildiraklar.
5. Qabul qilish x hozirgacha yozilgan doiralar soni bo'lishi uchun yozishni davom eting xn + 1 dan xn + n eng ichki doiradagi kontsentrik doiralarda, shunday qilib xn + 1 (x − 1)n + 1.
6. 5-bosqichni eng katta aylanish doirasi birinchi darajaga tekshiriladigan eng katta sonni qamrab olguncha takrorlang.
7. 1 raqamini urib qo'ying.
8. 1-qadamda topilgan va eng tashqi doiradagi (1-doirada) asosiy sonlarni urmasdan, barcha tashqi doiralarda 2-bosqichda qo'llaniladigan asosiy sonlarning spikerlarini urib qo'ying.
9. 4-bosqichda ichki aylanadan urilgan barcha ko'p sonli sonlarning ko'paytmalarini 8-qadamdagi asosiy sonlar pog'onalarini urish bilan urib tashlang.
10. G'ildirakdagi qolgan raqamlar asosan tub sonlardir (ular birgalikda "nisbatan" tub deb nomlanadi). Qolgan asosiy bo'lmaganlarni olib tashlash uchun Eratosfen elagi yoki undan kattaroq faktorizatsiya g'ildiraklarini qo'llash kabi boshqa usullardan foydalaning.

Misol

N = 2x3 = 6 bo'lgan g'ildirak faktorizatsiyasi

1. Birinchi 2 ta asosiy sonni toping: 2 va 3.

2. n = 2 × 3 = 6

3.

 1  2  3  4  5  6

4. 2 va 3 omillarni urib chiqing, ular 4 va 6 ni 2 omillari sifatida; 6, chunki 3 ning yagona omili allaqachon urilgan:

 1  2  3  4  5  6

5. x = 1.
xn + 1 = 1 · 6 + 1 = 7.
(x + 1)n = (1 + 1) · 6 = 12.
7 ga 12 ni 7 ga 1 ga tenglashtirilgan holda yozing.

 1  2  3  4  5  6 7  8  9 10 11 12

6. x = 2.
xn + 1 = 2 · 6 + 1 = 13.
(x + 1)n = (2 + 1) · 6 = 18.
13 dan 18 gacha yozing.
Keyingi qatorlarni takrorlang.

 1  2  3  4  5  6 7  8  9 10 11 1213 14 15 16 17 1819 20 21 22 23 2425 26 27 28 29 30

7 va 8. Elakdan o'tkazish

 1  2  3  4  5  6 7  8  9 10 11 1213 14 15 16 17 1819 20 21 22 23 2425 26 27 28 29 30

9. Elakdan o'tkazish

 1  2  3  4  5  6 7  8  9 10 11 1213 14 15 16 17 1819 20 21 22 23 2425 26 27 28 29 30

10. Olingan ro'yxat 25 ga teng bo'lmagan 25 ni o'z ichiga oladi, bu 5 ga teng². Unga etib borish uchun uni yo'q qilish uchun elak kabi boshqa usullardan foydalaning

2 3 5 7 11 13 17 19 23 29

Shuni esda tutingki, aynan keyingi g'ildirakning 5 ta tsiklining asosiy sonidan foydalanib va ​​natijaviy ro'yxatdagi ushbu asosiyning (va faqat shu asosiyning) ko'pini (larini) chiqarib, biz bazaga ega bo'lgan faktorizatsiya g'ildiragi uchun 4-qadam bo'yicha asosiy g'ildirakni oldik. 2, 3 va 5 sonlari; bu oldingi 2/3 faktorizatsiya g'ildiragidan oldin bitta g'ildirak. Keyingi 7 ta tsikldan foydalangan holda 10-bosqichga o'tilgan qadamlarni bajarish va natijada 10-bosqichdagi natijalarni faqatgina 7-ning ko'paytmalarini chiqarib tashlash (bu holda ba'zi bir "nisbiy" sonlarni qoldirish va ketma-ket barcha holatlarda, ya'ni ba'zilari to'g'ri emas) Keyingi rivojlangan g'ildirakni olish uchun, ketma-ket kattaroq g'ildiraklarni olish uchun zarur bo'lgan bosqichlarni rekursiv ravishda takrorlang.

Tahlil va kompyuterda amalga oshirish

Rasmiy ravishda, usul quyidagi tushunchalardan foydalanadi: Birinchidan, uning (cheksiz) ko'pliklarning to'plami bilan birlashtirilgan asosiy tublar to'plami tub sonlarning ustki qismi. Ikkinchidan, cheksiz koprmlar to'plamini koprmlardan asoslar to'plamigacha 2 va tayanch to'plam hosilalari orasida osonlik bilan sanab o'tish mumkin. (Shuni esda tutingki, 1 maxsus ishlov berishni talab qiladi.)

Yuqoridagi misolda ko'rinib turganidek, yuqoridagi rekursiv protsedurani 4 dan 10 gacha bo'lgan bosqichlarida takroriy qo'llanilishi natijasida istalgan saralash diapazonini qamrab oluvchi g'ildiraklar ro'yxati bo'lishi mumkin (unga qisqartirish mumkin) va natijada olingan ro'yxat faqat ko'paytmalarni o'z ichiga oladi. oxirgi ishlatilgan tayanch tub sonlardan bittadan yuqori sonlar.

E'tibor bering, g'ildirak elaklash diapazonining kerakli yuqori chegarasini bosib o'tgach, boshqa g'ildiraklarni ishlab chiqarishni to'xtatish va shu g'ildirakdagi ma'lumotlardan foydalanib, Eratosfen tipidagi texnikadan foydalangan holda, lekin so'nggi bo'shliqlar ro'yxatidan qolgan kompozit sonlarni chiqarib olish mumkin. ortiqcha ovlardan qochish uchun g'ildirakka xos naqsh; ba'zi bir optimallashtirishlarni (keyingi bobda isbotlangan) har qanday kompozitsion raqamni takroriy bekor qilinmasligi asosida amalga oshirish mumkin bo'lishi mumkin: qolgan har bir kompozitsiya aynan bir marta bekor qilinadi. Shu bilan bir qatorda, kerakli elak diapazonining kvadrat ildizigacha bo'lgan sonlar yordamida kesilgan g'ildiraklar ro'yxatlarini yaratishda davom etish mumkin, bu holda g'ildirakdagi qolgan barcha raqamlar asosiy bo'ladi; ammo, bu usul hech qachon kompozitsion raqamlarni bir martadan ko'proq yo'q qilmaslik kabi samarali bo'lsa-da, ketma-ket g'ildirakni tozalashda odatdagidek ko'rib chiqiladigan olib tashlash operatsiyalaridan tashqarida ko'p vaqtni yo'qotadi, shuning uchun ko'p vaqt talab etiladi. g'ildirak quyidagilarga asoslanadi: k> n sonini hisobga olgan holda, agar k mod n va n nisbatan tub bo'lmasa, k asosiy emasligini bilamiz. Shundan kelib chiqib, g'ildirak elagi olib tashlaydigan sonlarning ulushini aniqlash mumkin (garchi hammasi ham jismonan urilmasa ham; kam g'ildiraklarni kattaroq g'ildiraklarga nusxalash jarayonida ko'pchilik avtomatik ravishda o'chirilishi mumkin) 1 - phi (n) / n, bu ham elakning samaradorligi.

Ma'lumki

${displaystyle lim inf {frac {varphi (n)} {n}} log log n = e ^ {- gamma} sim 0.56145948,}$

qayerda γ bu Eyler doimiysi.^[5]Shunday qilib, phi (n) / n nolga boradi, chunki n cheksizlikka ko'payadi va bu samaradorlik cheksiz katta n uchun juda sekin 100% ga ko'tarilishini ko'rish mumkin.Fi ning xususiyatlaridan, eng samarali ekanligini osongina ko'rish mumkin. x dan kichikroq elak bu erda ${displaystyle n = p_ {1} p_ {2} ... p_ {i}$ va ${displaystyle np_ {i + 1} geq x}$ (ya'ni g'ildirak avlodi oxirgi g'ildirak o'tganida to'xtab qolishi yoki elaklash oralig'ida eng yuqori sonni kiritish uchun etarlicha aylanaga ega bo'lishi mumkin).

Kompyuterda maksimal darajada foydalanish uchun biz n dan kichikroq va to'plam sifatida unga nisbatan asosiy sonlarni istaymiz. Bir nechta kuzatishlar yordamida to'plamni osongina yaratish mumkin:

1. Bilan boshlang ${displaystyle S_ {1} = {1}}$, bu uchun o'rnatilgan ${displaystyle n = 1}$ birinchi bosh sifatida 2 bilan. Ushbu dastlabki to'plam, ikkitadan boshlanadigan barcha raqamlar "nisbiy" sonlar qatoriga kiritilganligini anglatadi, chunki g'ildirak aylanasi 1 ga teng.
2. Quyidagi to'plamlar ${displaystyle S_ {2} = {1}}$ demak u hamma toq sonlar uchun 3 dan boshlanadi va 2 omillari chiqarib tashlanadi (aylanasi 2), ${displaystyle S_ {6} = {1,5}}$ yuqoridagi misolda dastlabki tayanch g'ildirakka nisbatan 2 va 3 faktorlar yo'q qilingan (atrofi 6).
3. Ruxsat bering ${displaystyle S_ {n} + k}$ ning har bir elementiga k qo'shilgan to'plam bo'ling ${displaystyle S_ {n}}$.
4. Keyin ${displaystyle S_ {np_ {i + 1}} = F_ {p_ {i + 1}} [S_ {n} chashka S_ {n} + ncup S_ {n} + 2ncup ... chashka S_ {n} + n ( p_ {i + 1} -1)]}$ qayerda ${displaystyle F_ {x}}$ x ning barcha ko'paytmalarini olib tashlash operatsiyasini ifodalaydi.
5. 1 va ${displaystyle p_ {i + 1}}$ eng kichigi ikkitasi bo'ladi ${displaystyle S_ {n}}$ qachon ${displaystyle n> 2}$ oddiy sonlarni alohida-alohida hisoblash zaruratini olib tashlash, ammo algoritmda keyingi ketma-ketliklarga kiritilmagan barcha o'chirilgan asosiy asoslarni yozib olish kerak.
6. N> 2 atrofi nosimmetrik bo'lgan barcha to'plamlar ${displaystyle n / 2}$, saqlash talablarini kamaytirish. Quyidagi algoritmda bu fakt ishlatilmaydi, lekin u har bir to'plamdagi ketma-ket sonlar orasidagi bo'shliqlar yarim nuqta atrofida nosimmetrik bo'lishiga asoslanadi.

Shuningdek qarang

• Sundaram elagi
• Atkin elagi
• Elak nazariyasi

Adabiyotlar

Tashqi havolalar

• G'ildiraklarni ishlab chiqarish
• Boshlang'ich raqamli elaklarni yaxshilandi Pol Pritchard tomonidan