Gamma funktsiyasi - Gamma function

Haqiqiy o'qning bir qismi bo'ylab gamma funktsiyasi

Yilda matematika, gamma funktsiyasi (tomonidan ko'rsatilgan ${displaystyle Gamma,}$ katta harf gamma dan Yunon alifbosi ) ning keng tarqalgan ishlatiladigan kengaytmalaridan biridir faktorial funktsiya ga murakkab sonlar. Gamma funktsiyasi musbat bo'lmagan butun sonlardan tashqari barcha murakkab sonlar uchun aniqlanadi. Har qanday kishi uchun musbat tamsayı ${displaystyle n,}$

{displaystyle Gamma (n) = (n-1)! .}

Tomonidan olingan Daniel Bernulli, haqiqiy qismi ijobiy bo'lgan murakkab sonlar uchun gamma funktsiyasi konvergent orqali aniqlanadi noto'g'ri integral:

{displaystyle Gamma (z) = int _ {0} ^ {infty} x ^ {z-1} e ^ {- x}, dx, qquad Re (z)> 0.}

Keyin gamma funktsiyasi quyidagicha aniqlanadi analitik davomi Ushbu ajralmas funktsiyani a meromorfik funktsiya anavi holomorfik funktsiyasi oddiy bo'lgan nol va salbiy butun sonlardan tashqari butun kompleks tekislikda qutblar.

Gamma funktsiyasi nolga ega emas, shuning uchun o'zaro gamma funktsiyasi ${displaystyle 1 / Gamma}$ bu butun funktsiya. Aslida, gamma funktsiyasi Mellin o'zgarishi salbiy eksponent funktsiya:

{displaystyle Gamma (z) = {{mathcal {M}} e ^ {- x}} (z).}

Faktorial funktsiyaning boshqa kengaytmalari mavjud, ammo gamma funktsiyasi eng ommabop va foydalidir. Bu turli xil ehtimollarni taqsimlash funktsiyalarining tarkibiy qismidir va shu sababli u maydonlarida amal qiladi ehtimollik va statistika, shu qatorda; shu bilan birga kombinatorika.

Motivatsiya

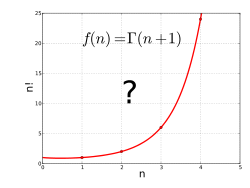
Gamma funktsiyasi faktorial funktsiyani butun bo'lmagan qiymatlarga interpolatsiya qiladi.

Gamma funktsiyasini quyidagilarning echimi sifatida ko'rish mumkin interpolatsiya muammo:

"A toping silliq egri chiziq nuqtalarni bir-biriga bog'laydigan

{displaystyle (x, y)}

tomonidan berilgan

{displaystyle y = (x-1)!}

uchun musbat tamsayı qiymatlarida

{displaystyle x}

."

Birinchi bir necha faktoriallarning chizmasi shuni ko'rsatadiki, bunday egri chizish mumkin, ammo egri chiziqni aniq tavsiflaydigan formulaga ega bo'lish afzalroq bo'ladi, bunda amallar soni kattaligiga bog'liq emas ${displaystyle x}$ . Faktorial uchun oddiy formula, ${displaystyle x! = 1 imes 2 imes cdots imes x}$ , ning to'g'ridan-to'g'ri kasr qiymatlari uchun ishlatib bo'lmaydi ${displaystyle x}$ chunki u faqat qachon amal qiladi $x$ a tabiiy son (yoki musbat tamsayı). Nisbatan aytganda, faktoriallar uchun bunday oddiy echimlar mavjud emas; summalar, mahsulotlar, kuchlarning cheklangan kombinatsiyasi yo'q, eksponent funktsiyalar, yoki logarifmlar ifodalash uchun etarli bo'ladi ${displaystyle x!}$ ; kabi vositalar yordamida faktoriallarning umumiy formulasini topish mumkin integrallar va chegaralar dan hisob-kitob. Buning yaxshi echimi gamma funktsiyasidir.^[1]

Faktorialning butun bo'lmagan sonlarga qadar uzluksiz kengaytmalari mavjud: har qanday ajratilgan nuqtalar to'plami orqali cheksiz ko'p egri chiziqlarni o'tkazish mumkin. Gamma funktsiyasi amalda eng foydali echimdir analitik (musbat bo'lmagan sonlardan tashqari) va uni bir necha ekvivalent usullar bilan aniqlash mumkin. Biroq, faktorialni kengaytiradigan yagona analitik funktsiya emas, chunki unga musbat tamsayılarda nolga teng bo'lgan har qanday analitik funktsiyani qo'shadi. $k gunoh m π x$ , bu xususiyat bilan yana bir funktsiyani beradi.^[1]

Gamma funktsiyasi,

Γ (z)

bilan birga chizilgan ko'k rangda

Γ (z) + gunoh (π z)

yashil rangda. Ijobiy tamsayılarda kesishuvga e'tibor bering, ikkalasi ham faktoriallarning haqiqiy bo'lmagan analitik davomi

Yuqoridagi interpolatsiyani qondirishdan ko'ra ko'proq cheklovchi xususiyat - bu qondirishdir takrorlanish munosabati faktorial funktsiyaning tarjima qilingan versiyasini aniqlash,^[2]^[3]

{displaystyle f (1) = 1,}

{displaystyle f (x + 1) = xf (x),}

har qanday ijobiy haqiqiy raqam uchun $x$ . Ammo bu har qanday davriy analitik funktsiyani ko'paytirishga imkon beradi, masalan, musbat butun sonlarda 1 ga teng $e k gunoh m π x$ . Ikkilanishlarni nihoyat hal qilishning bir necha usullaridan biri Bor-Mollerup teoremasi. Unda aytilishicha, qachonki shart $f$ bo'lishi logaritmik konveks (yoki "o'ta konveks"^[4]) qo'shiladi, u o'ziga xos tarzda aniqlanadi $f$ ijobiy, haqiqiy kirishlar uchun. U erdan gamma funktsiyasini noyob va noldan tashqari barcha haqiqiy va murakkab qiymatlarga (salbiy butun sonlardan va noldan tashqari) kengaytirish mumkin. analitik davomi ning $f$ .^[5]

Ta'rif

Asosiy ta'rif

Notation ${displaystyle Gamma (z)}$ tufayli Legendre.^[1] Agar kompleks sonning haqiqiy qismi bo'lsa $z$ ijobiy ( ${displaystyle Re (z)> 0}$ ), keyin ajralmas

{displaystyle Gamma (z) = int _ {0} ^ {infty} x ^ {z-1} e ^ {- x}, dx}

mutlaqo birlashadi, va sifatida tanilgan Ikkinchi turdagi Eyler integrali. (Eylerning birinchi turining ajralmas qismi bu beta funktsiyasi.^[1]) Foydalanish qismlar bo'yicha integratsiya, buni ko'radi:

{displaystyle {egin {aligned} Gamma (z + 1) & = int _ {0} ^ {infty} x ^ {z} e ^ {- x}, dx & = {Big [} -x ^ {z} e ^ {- x} {Big]} _ {0} ^ {infty} + int _ {0} ^ {infty} zx ^ {z-1} e ^ {- x}, dx & = lim _ {x o infty} (- x ^ {z} e ^ {- x}) - (- 0 ^ {z} e ^ {- 0}) + zint _ {0} ^ {infty} x ^ {z-1} e ^ {- x}, dx.end {hizalanmış}}}

Buni tan olish ${displaystyle -x ^ {z} e ^ {- x} o 0}$ kabi ${displaystyle x o infty,}$

{displaystyle {egin {aligned} Gamma (z + 1) & = zint _ {0} ^ {infty} x ^ {z-1} e ^ {- x}, dx & = zGamma (z) .end {aligned }}}

Biz hisoblashimiz mumkin ${displaystyle Gamma (1) {ext {:}}}$

{displaystyle {egin {aligned} Gamma (1) & = int _ {0} ^ {infty} x ^ {1-1} e ^ {- x}, dx & = {Big [} -e ^ {- x } {Katta]} _ {0} ^ {infty} & = lim _ {x o infty} (- e ^ {- x}) - (- e ^ {- 0}) & = 0 - (- 1 ) & = 1.end {aligned}}}

Sharti bilan; inobatga olgan holda ${displaystyle Gamma (1) = 1}$ va ${displaystyle Gamma (n + 1) = nGamma (n),}$

{displaystyle Gamma (n) = 1cdot 2cdot 3cdots (n-1) = (n-1)!}

barcha musbat sonlar uchun $n$ . Buni misol sifatida ko'rish mumkin induksiya bilan isbotlash.

Shaxsiyat ${extstyle Gamma (z) = {frac {Gamma (z + 1)} {z}}}$ ishlatilishi mumkin (yoki xuddi shu natijani beradigan, analitik davomi uchun integral formulasini noyob tarzda kengaytirish uchun foydalanish mumkin) ${displaystyle Gamma (z)}$ a meromorfik funktsiya barcha murakkab sonlar uchun aniqlangan $z$ , noldan kam yoki teng bo'lgan butun sonlardan tashqari.^[1] Odatda gamma funktsiyasi deb ataladigan ushbu kengaytirilgan versiya.^[1]

Muqobil ta'riflar

Eylerning cheksiz mahsulot sifatida ta'rifi

Taxminan taxmin qilayotganda ${displaystyle z!}$ murakkab raqam uchun ${displaystyle z}$ , avval hisoblash samarali bo'ladi ${displaystyle n!}$ ba'zi katta butun sonlar uchun ${displaystyle n}$ . Buning qiymatini taxmin qilish uchun foydalaning ${displaystyle (n + z)!}$ , keyin esa rekursiya aloqasidan foydalaning ${displaystyle m! = m (m-1)!}$ orqaga ${displaystyle n}$ marta, uni taxminiy ravishda ochish uchun ${displaystyle z!}$ . Bundan tashqari, bu taxminiy chegarada aniq ${displaystyle n}$ cheksizlikka boradi.

Xususan, sobit butun son uchun ${displaystyle m}$ , bu shunday

{displaystyle lim _ {n o infty} {frac {n!; (n + 1) ^ {m}} {(n + m)!}} = 1 ,.}

Agar ${displaystyle m}$ tamsayı emas, demak, bu tenglama to'g'ri yoki yo'qligini aytish mumkin emas, chunki biz hali (ushbu bo'limda) tamsayı bo'lmaganlar uchun faktorial funktsiyani aniqlamadik. Biroq, biz faktorial funktsiyani o'zboshimchalik bilan butun sonni ushlab turishda davom ettirishni talab qilib, tamsayı bo'lmagan sonlarga noyob kengaytmasini olamiz. ${displaystyle m}$ ixtiyoriy kompleks son bilan almashtiriladi ${displaystyle z}$ .

{displaystyle lim _ {n o infty} {frac {n!; (n + 1) ^ {z}} {(n + z)!}} = 1 ,.}

Ikkala tomonni ko'paytiring ${displaystyle z!}$ beradi

{displaystyle {egin {aligned} z! & = lim _ {n o infty} n! {frac {z!} {(n + z)!}} (n + 1) ^ {z} [8pt] & = lim _ {n o infty} (1cdots n) {frac {1} {(1 + z) cdots (n + z)}} chap (chap ({frac {2} {1}} ight) chap ({frac { 3} {2}} ight) cdots qoldi ({frac {n + 1} {n}} ight) ight) ^ {z} [8pt] & = prod _ {n = 1} ^ {infty} chap [{ frac {1} {1+ {frac {z} {n}}}} chap (1+ {frac {1} {n}} ight) ^ {z} ight] .end {aligned}}}

Bu cheksiz mahsulot barcha murakkab sonlar uchun yaqinlashadi ${displaystyle z}$ manfiy tamsayılardan tashqari ${displaystyle m! = m (m-1)!}$ qiymat orqali orqaga qarab ${displaystyle m = 0}$ nolga bo'linishni o'z ichiga oladi.

Xuddi shunday gamma funktsiyasi uchun ham, cheksiz mahsulot sifatida ta'rifi Eyler barcha murakkab raqamlar uchun amal qiladi ${displaystyle z}$ musbat bo'lmagan sonlardan tashqari:

{displaystyle Gamma (z) = {frac {1} {z}} prod _ {n = 1} ^ {infty} {frac {left (1+ {frac {1} {n}} ight) ^ {z}} {1+ {frac {z} {n}}}} ,.}

Ushbu konstruktsiyaga ko'ra, gamma funktsiyasi bir vaqtning o'zida qondiradigan noyob funktsiyadir ${displaystyle Gamma (1) = 1}$ , ${displaystyle Gamma (z + 1) = zGamma (z)}$ barcha murakkab sonlar uchun ${displaystyle z}$ musbat bo'lmagan tamsayılardan tashqari va ${extstyle lim _ {n o infty} {frac {Gamma (n + z)} {Gamma (n); n ^ {z}}} = 1}$ barcha murakkab sonlar uchun ${displaystyle z}$ .^[1]

Vaystrashtning ta'rifi

Tufayli gamma funktsiyasi uchun ta'rif Weierstrass barcha murakkab raqamlar uchun ham amal qiladi $z$ musbat bo'lmagan sonlardan tashqari:

{displaystyle Gamma (z) = {frac {e ^ {- gamma z}} {z}} prod _ {n = 1} ^ {infty} chap (1+ {frac {z} {n}} ight) ^ { -1} e ^ {z / n},}

qayerda ${displaystyle gamma taxminan 0,577216}$ bo'ladi Eyler-Maskeroni doimiysi.^[1] Bu Hadamard mahsuloti ning ${displaystyle 1 / Gamma (z)}$ qayta yozilgan shaklda. Darhaqiqat, beri ${displaystyle 1 / Gamma (z)}$ bu butun 1-turdagi oddiy nol bilan ${displaystyle z = 0}$ , bizda mahsulot vakili mavjud

{displaystyle {frac {1} {Gamma (z)}} = ze ^ {Az + B} prod _ {ho} left (1- {frac {z} {ho}} ight) e ^ {z / ho}, }

bu erda mahsulot noldan oshib ketadi ${displaystyle ho eq 0}$ ning ${displaystyle 1 / Gamma (z)}$ . Beri ${displaystyle Gamma (z)}$ musbat bo'lmagan tamsayılarda oddiy qutblarga ega, u quyidagicha ${displaystyle 1 / Gamma (z)}$ musbat bo'lmagan tamsayılarda oddiy nollarga ega va shuning uchun yuqoridagi tenglama Weierstrass formulasiga aylanadi ${displaystyle -Az-B}$ o'rniga ${displaystyle -gamma z}$ . Konstantalarning hosilasi ${displaystyle A = gamma}$ va ${displaystyle B = 0}$ ba'zi bir texnik xususiyatga ega, ammo ba'zi bir xususiyatlardan foydalangan holda amalga oshirilishi mumkin Riemann zeta funktsiyasi (qarang bu o'ziga xoslik, masalan; misol uchun). Shuningdek qarang Vaystrasht faktorizatsiya teoremasi.

Umumlashtirilgan Laguer polinomlari bo'yicha

Ning vakili to'liq bo'lmagan gamma funktsiyasi xususida umumlashtirilgan Laguer polinomlari bu

{displaystyle Gamma (z, x) = x ^ {z} e ^ {- x} sum _ {n = 0} ^ {infty} {frac {L_ {n} ^ {(z)} (x)} {n +1}},}

uchun yaqinlashadigan ${displaystyle Re (z)> - 1}$ va ${displaystyle x> 0}$ .^[6]

Xususiyatlari

Umumiy

Gamma funktsiyasi uchun boshqa muhim funktsional tenglamalar Eyler aks ettirish formulasi

{displaystyle Gamma (1-z) Gamma (z) = {pi over sin (pi z)}, qquad zot in mathbb {Z}}

shuni anglatadiki

{displaystyle Gamma (varepsilon -n) = (- 1) ^ {n-1}; {frac {Gamma (-varepsilon) Gamma (1 + varepsilon)} {Gamma (n + 1-varepsilon)}},}

va Legendre takrorlash formulasi

{displaystyle Gamma (z) Gamma chap (z + {frac {1} {2}} ight) = 2 ^ {1-2z}; {sqrt {pi}}; Gamma (2z).}

Eyler aks ettirish formulasini chiqarish

Beri ${displaystyle e ^ {- t} = lim _ {n o infty} chap (1- {frac {t} {n}} ight) ^ {n},}$

gamma funktsiyasini quyidagicha ifodalash mumkin

{displaystyle Gamma (z) = lim _ {n o infty} int _ {0} ^ {n} t ^ {z-1} chap (1- {frac {t} {n}} ight) ^ {n}, dt.}

Qismlarga qarab birlashtiriladi ${displaystyle n}$ marta hosil beradi

{displaystyle Gamma (z) = lim _ {n o infty} {frac {n} {nz}} cdot {frac {n-1} {n (z + 1)}} cdot {frac {n-2} {n (z + 2)}} cdots {frac {1} {n (z + n-1)}} int _ {0} ^ {n} t ^ {z + n-1}, dt,}

bu tengdir

{displaystyle Gamma (z) = lim _ {n o infty} {frac {n!} {n ^ {n}}} prod _ {k = 0} ^ {n} (z + k) ^ {- 1} n ^ {z + n}.}

Buni shunday yozish mumkin

{displaystyle Gamma (z) = lim _ {n o infty} {frac {n ^ {z}} {z}} prod _ {k = 1} ^ {n} {frac {k} {z + k}} = lim _ {n o infty}} frac {n ^ {z}} {z}} prod _ {k = 1} ^ {n} {frac {1} {1+ {frac {z} {k}}}} .}

Keyin, gamma funktsiyasining funktsional tenglamasidan foydalanib, biz olamiz

{displaystyle -zGamma (-z) Gamma (z) = Gamma (1-z) Gamma (z) = lim _ {n o infty} {frac {1} {z}} prod _ {k = 1} ^ {n } {frac {1} {1- {frac {z ^ {2}} {k ^ {2}}}}}.}

Bu bo'lishi mumkin isbotlangan bu

{displaystyle sin (pi z) = pi zprod _ {k = 1} ^ {infty} chap (1- {frac {z ^ {2}} {k ^ {2}}} ight).}

Keyin

{displaystyle {frac {pi} {sin (pi z)}} = lim _ {n o infty}} frac {1} {z}} prod _ {k = 1} ^ {n} {frac {1} {1 - {frac {z ^ {2}} {k ^ {2}}}}}.}

Eyler aks ettirish formulasi quyidagicha:

{displaystyle Gamma (1-z) Gamma (z) = {frac {pi} {sin (pi z)}}, qquad zot in mathbb {Z}.}

Legendre takrorlanish formulasini chiqarish

The beta funktsiyasi sifatida ifodalanishi mumkin

{displaystyle mathrm {B} (z_ {1}, z_ {2}) = {frac {Gamma (z_ {1}) Gamma (z_ {2})} {Gamma (z_ {1} + z_ {2})} } = int _ {0} ^ {1} t ^ {z_ {1} -1} (1-t) ^ {z_ {2} -1}, dt.}

O'rnatish ${displaystyle z_ {1} = z_ {2} = z}$ hosil

{displaystyle {frac {Gamma ^ {2} (z)} {Gamma (2z)}} = int _ {0} ^ {1} t ^ {z-1} (1-t) ^ {z-1}, dt.}

O'zgarishdan keyin ${displaystyle t = {frac {1 + x} {2}}}$ biz olamiz

{displaystyle {frac {Gamma ^ {2} (z)} {Gamma (2z)}} = {frac {1} {2 ^ {2z-1}}} int _ {- 1} ^ {1} chap (1 -x ^ {2} tun) ^ {z-1}, dx.}

Funktsiya ${displaystyle (1-x ^ {2}) ^ {z-1}}$ hatto, shuning uchun ham

{displaystyle 2 ^ {2z-1} Gamma ^ {2} (z) = 2Gamma (2z) int _ {0} ^ {1} (1-x ^ {2}) ^ {z-1}, dx.}

Endi faraz qiling

{displaystyle mathrm {B} chap ({frac {1} {2}}, zight) = int _ {0} ^ {1} t ^ {{frac {1} {2}} - 1} (1-t) ^ {z-1}, dt, quad t = s ^ {2}.}

Keyin

{displaystyle mathrm {B} chap ({frac {1} {2}}, zight) = 2int _ {0} ^ {1} (1-s ^ {2}) ^ {z-1}, ds = 2int _ {0} ^ {1} (1-x ^ {2}) ^ {z-1}, dx.}

Bu shuni anglatadi

{displaystyle 2 ^ {2z-1} Gamma ^ {2} (z) = Gamma (2z) mathrm {B} chap ({frac {1} {2}}, zight).}

Beri

{displaystyle mathrm {B} chap ({frac {1} {2}}, zight) = {frac {Gamma chap ({frac {1} {2}} ight) Gamma (z)} {Gamma chap (z + {frac) {1} {2}} tun)}}, to'rtta Gamma chapda ({frac {1} {2}} ight) = {sqrt {pi}},}

Legendre takrorlash formulasi quyidagicha:

{displaystyle Gamma (z) Gamma chap (z + {frac {1} {2}} ight) = 2 ^ {1-2z} {sqrt {pi}}; Gamma (2z).}

Ikki nusxadagi formulalar ko'paytirish teoremasi (Qarang,^[6] Tenglama 5.5.6)

{displaystyle prod _ {k = 0} ^ {m-1} Gamma qoldi (z + {frac {k} {m}} ight) = (2pi) ^ {frac {m-1} {2}}; m ^ { {frac {1} {2}} - mz}; Gamma (mz).}

Limit ta'rifidan ko'rinadigan oddiy, ammo foydali xususiyat quyidagilardir:

{displaystyle {overline {Gamma (z)}} = Gamma ({overline {z}}); Rightarrow; Gamma (z) Gamma ({overline {z}}) in mathbb {R}.}

Xususan, bilan $z = a + bi$ , bu mahsulot

{displaystyle | Gamma (a + bi) | ^ {2} = | Gamma (a) | ^ {2} prod _ {k = 0} ^ {infty} {frac {1} {1+ {frac {b ^ { 2}} {(a + k) ^ {2}}}}}}

Agar haqiqiy qism butun yoki yarim tamsayı bo'lsa, bu son bilan ifodalanishi mumkin yopiq shakl:

{displaystyle {egin {aligned} | Gamma (bi) | ^ {2} & = {frac {pi} {bsinh (pi b)}} [6pt] | Gamma chap ({frac {1} {2}} + biight) | ^ {2} & = {frac {pi} {cosh (pi b)}} | Gamma chap (1 + biight) | ^ {2} & = {frac {pi b} {sinh (pi b) }} | Gamma chap (1 + n + biight) | ^ {2} & = {frac {pi b} {sinh (pi b)}} prod _ {k = 1} ^ {n} chap (k ^ { 2} + b ^ {2} ight), quad nin mathbb {N} | Gamma chap (-n + biight) | ^ {2} & = {frac {pi} {bsinh (pi b)}} prod _ { k = 1} ^ {n} chap (k ^ {2} + b ^ {2} ight) ^ {- 1}, quad nin mathbb {N} | Gamma chap ({frac {1} {2}} pm) n + biight) | ^ {2} & = {frac {pi} {cosh (pi b)}} prod _ {k = 1} ^ {n} chap (chap (k- {frac {1} {2}}) ight) ^ {2} + b ^ {2} ight) ^ {pm 1}, quad nin mathbb {N} end {hizalangan}}}

To'liq yoki yarim tamsayı haqiqiy qism uchun formulalarni tasdiqlash

Birinchidan, qo'llaniladigan aks ettirish formulasini ko'rib chiqing ${displaystyle z = bi}$ .

{displaystyle Gamma (bi) Gamma (1-bi) = {frac {pi} {sin (pi bi)}}}

Takrorlanish munosabatini ikkinchi davrga nisbatan qo'llasak, bizda

{displaystyle -bicdot Gamma (bi) Gamma (-bi) = {frac {pi} {sin (pi bi)}}}

bu oddiy qayta qurish bilan beradi

{displaystyle Gamma (bi) Gamma (-bi) = {frac {pi} {- bisin (pi bi)}} = {frac {pi} {bsinh (pi b)}}}

Ikkinchidan, qo'llaniladigan aks ettirish formulasini ko'rib chiqing ${displaystyle z = {frac {1} {2}} + bi}$ .

{displaystyle Gamma ({frac {1} {2}} + bi) Gamma chap (1 - ({frac {1} {2}} + bi) ight) = Gamma ({frac {1} {2}} + bi) ) Gamma ({frac {1} {2}} - bi) = {frac {pi} {sin left (pi ({frac {1} {2}} + bi) ight)}} = {frac {pi} { cos (pi bi)}} = {frac {pi} {cosh (pi b)}}}

Ning boshqa qiymatlari uchun formulalar ${displaystyle z}$ buning uchun haqiqiy qism butun yoki yarim tamsayı bo'lib, tezda bajariladi induksiya ijobiy va salbiy yo'nalishlarda takrorlanish munosabatlaridan foydalanish.

Ehtimol, tamsayı bo'lmagan argumentda gamma funktsiyasining eng yaxshi ma'lum bo'lgan qiymati

{displaystyle Gamma chap ({frac {1} {2}} ight) = {sqrt {pi}},}

sozlash orqali topish mumkin ${extstyle z = {frac {1} {2}}}$ aks ettirish yoki takrorlash formulalarida, ga munosabati yordamida beta funktsiyasi bilan quyida berilgan ${extstyle x = y = {frac {1} {2}}}$ , yoki oddiygina almashtirish bilan ${displaystyle u = {sqrt {x}}}$ gamma funktsiyasining integral ta'rifida, natijada a Gauss integrali. Umuman olganda, ning manfiy bo'lmagan tamsayı qiymatlari uchun ${displaystyle n}$ bizda ... bor:

{displaystyle {egin {aligned} Gamma chap ({frac {1} {2}} + kecha) va = {(2n)! 4 ^ {n} n!} {sqrt {pi}} = {frac {(2n-1) !!} {2 ^ {n}}} {sqrt {pi}} = {inom {n- {frac { 1} {2}}} {n}} n! {Sqrt {pi}} [8pt] Gamma qoldi ({frac {1} {2}} - kecha) & = {(- 4) ^ {n} n ! ustidan (2n)!} {sqrt {pi}} = {frac {(-2) ^ {n}} {(2n-1) !!}} {sqrt {pi}} = {frac {sqrt {pi}} {{inom {-1/2} {n}} n!}} oxiri {hizalanmış}}}

qayerda ${displaystyle n !!}$ belgisini bildiradi ikki faktorial ning n va qachon ${displaystyle n = 0}$ , ${displaystyle n !! = 1}$ . Qarang Gamma funktsiyasining alohida qiymatlari hisoblangan qiymatlar uchun.

Buning natijasini umumlashtirish istagi paydo bo'lishi mumkin ${extstyle Gamma chapda ({frac {1} {2}} ight) = {sqrt {pi}}}$ boshqa individual qadriyatlar uchun formulani izlash orqali ${displaystyle Gamma (r)}$ qayerda ${displaystyle r}$ oqilona, ayniqsa, chunki Gaussning digamma teoremasi, buni yaqindan bog'liq bo'lganlar uchun qilish mumkin digamma funktsiyasi har qanday oqilona qiymatga ega. Biroq, bu raqamlar ${displaystyle Gamma (r)}$ elementar funktsiyalar nuqtai nazaridan o'zlari tomonidan ifodalanishi ma'lum emas. Bu isbotlangan ${displaystyle Gamma (n + r)}$ a transandantal raqam va algebraik jihatdan mustaqil ning ${displaystyle pi}$ har qanday butun son uchun ${displaystyle n}$ va kasrlarning har biri ${extstyle r = {frac {1} {6}}, {frac {1} {4}}, {frac {1} {3}}, {frac {2} {3}}, {frac {3} { 4}}, {frac {5} {6}}}$ .^[7] Umuman olganda, gamma funktsiyasining qiymatlarini hisoblashda biz raqamli yaqinlashishga qaror qilishimiz kerak.

Asimptotik yaqinlashishning yana bir foydali chegarasi:

{displaystyle lim _ {n o infty} {frac {Gamma (n + alfa)} {Gamma (n) n ^ {alfa}}} = 1, qquad alfa in mathbb {C}.}

Gamma funktsiyasining hosilalari poligamma funktsiyasi. Masalan:

{displaystyle Gamma '(z) = Gamma (z) psi _ {0} (z).}

Ijobiy tamsayı uchun $m$ gamma funktsiyasining hosilasini quyidagicha hisoblash mumkin (bu erda ${displaystyle gamma}$ bo'ladi Eyler-Maskeroni doimiysi ):

{displaystyle Gamma '(m + 1) = m! chap (-gamma + sum _ {k = 1} ^ {m} {frac {1} {k}} ight) ,.}

Uchun ${displaystyle Re (x)> 0}$ The ${displaystyle n}$ gamma funktsiyasining hosilasi:

Funktsiyaning hosilasi

Γ (z)

{displaystyle {frac {d ^ {n}} {dx ^ {n}}} Gamma (x) = int _ {0} ^ {infty} t ^ {x-1} e ^ {- t} (ln t) ^ {n}, dt.}

(Buni gamma funktsiyasining integral shaklini nisbatan farqlash orqali olish mumkin ${displaystyle x}$ va texnikasidan foydalangan holda integral belgisi ostida farqlash.)

Shaxsiyatdan foydalanish

{displaystyle Gamma ^ {(n)} (1) = (- 1) ^ {n} n! sum chegaralari _ {pi, vdash, n}, prod _ {i = 1} ^ {r} {frac {zeta ^ {*} (a_ {i})} {k_ {i}! cdot a_ {i}}} qquad zeta ^ {*} (x): = {egin {case} zeta (x) & xeq 1 gamma & x = 1end {holatlar}}}

qayerda ${displaystyle zeta (z)}$ bo'ladi Riemann zeta funktsiyasi va ${displaystyle pi}$ a bo'lim ning ${displaystyle n}$ tomonidan berilgan

{displaystyle pi = underbrace {a_ {1} + cdots + a_ {1}} _ {k_ {1} {ext {Terms}}} + cdots + underbrace {a_ {r} + cdots + a_ {r}} _ { k_ {r} {ext {atamalari}}},}

bizda, xususan

{displaystyle Gamma (z) = {frac {1} {z}} - gamma + {frac {1} {2}} chap (gamma ^ {2} + {frac {pi ^ {2}} {6}} tun ) z- {frac {1} {6}} chap (gamma ^ {3} + {frac {gamma pi ^ {2}} {2}} + 2zeta (3) ight) z ^ {2} + O (z ^ {3}).}

Tengsizliklar

Ijobiy haqiqiy sonlar bilan cheklangan bo'lsa, gamma funktsiyasi qat'iydir logaritmik konveks funktsiyasi. Ushbu xususiyat quyidagi uchta teng usullardan birida ko'rsatilishi mumkin:

Har qanday ikkita ijobiy haqiqiy son uchun ${displaystyle x_ {1}}$ va ${displaystyle x_ {2}}$ va har qanday kishi uchun ${displaystyle kalay [0,1]}$ ,

{displaystyle Gamma (tx_ {1} + (1-t) x_ {2}) leq Gamma (x_ {1}) ^ {t} Gamma (x_ {2}) ^ {1-t}.}

Har qanday ikkita ijobiy haqiqiy son uchun $x$ va $y$ bilan $y > x$ ,

{displaystyle left ({frac {Gamma (y)} {Gamma (x)}} ight) ^ {frac {1} {yx}}> exp left ({frac {Gamma '(x)} {Gamma (x)}) } yaxshi).}

Har qanday ijobiy haqiqiy raqam uchun ${displaystyle x}$ ,

{displaystyle Gamma '' (x) Gamma (x)> Gamma '(x) ^ {2}.}

Ushbu bayonotlarning oxirgisi, ta'rifi bo'yicha, xuddi shu bayonot bilan bir xil ${displaystyle psi ^ {(1)} (x)> 0}$ , qayerda ${displaystyle psi ^ {(1)}}$ bo'ladi poligamma funktsiyasi tartib 1. Gamma funktsiyasining logaritmik konveksiyasini isbotlash uchun shuni kuzatish kifoya ${displaystyle psi ^ {(1)}}$ ijobiy real uchun ketma-ket tasvirga ega $x$ , faqat ijobiy atamalardan iborat.

Logaritmik konveksiya va Jensen tengsizligi birgalikda har qanday ijobiy haqiqiy sonlarni nazarda tutadi ${displaystyle x_ {1}, ldots, x_ {n}}$ va ${displaystyle a_ {1}, ldots, a_ {n}}$ ,

{displaystyle Gamma chap ({frac {a_ {1} x_ {1} + cdots + a_ {n} x_ {n}} {a_ {1} + cdots + a_ {n}}} ight) leq {igl (} Gamma (x_ {1}) ^ {a_ {1}} cdots Gamma (x_ {n}) ^ {a_ {n}} {igr)} ^ {frac {1} {a_ {1} + cdots + a_ {n} }}.}

Shuningdek, gamma funktsiyalarining nisbati chegaralari mavjud. Eng taniqli Gautschining tengsizligi, bu har qanday ijobiy haqiqiy raqam uchun aytiladi $x$ va har qanday $s \in (0, 1)$ ,

{displaystyle x ^ {1-s} <{frac {Gamma (x + 1)} {Gamma (x + s)}} <(x + 1) ^ {1-s}.}

Stirling formulasi

Gamma funktsiyasini kompleks tekislikda aks ettirish. Har bir nuqta

{displaystyle z}

argumentiga ko'ra ranglanadi

{displaystyle Gamma (z)}

. Modulning kontur chizmasi

{displaystyle | Gamma (z) |}

ham ko'rsatiladi.

Kompleks gamma funktsiyasining mutlaq qiymatining 3 o'lchovli chizmasi

Ning xatti-harakati ${displaystyle Gamma (z)}$ ortib borayotgan ijobiy o'zgaruvchiga oddiy. Aslida eksponent funktsiyadan tez va tez o'sadi. Asimptotik tarzda ${extstyle z o infty,}$ gamma funktsiyasining kattaligi tomonidan berilgan Stirling formulasi

{displaystyle Gamma (z + 1) sim {sqrt {2pi z}} chap ({frac {z} {e}} ight) ^ {z},}

qaerda belgi ${displaystyle sim}$ asimptotik yaqinlashishni nazarda tutadi. Boshqacha qilib aytganda, ikki tomonning nisbati 1 ga yaqinlashadi ${extstyle z o + infty}$ .^[1]

Qoldiqlar

Ijobiy bo'lmaganlarning harakati ${displaystyle z}$ yanada murakkabroq. Eyler integrali yaqinlashmaydi ${displaystyle zleq 0}$ , ammo ijobiy kompleks yarim tekislikda aniqlaydigan funktsiya o'ziga xos xususiyatga ega analitik davomi salbiy yarim tekislikka. Analitik davom ettirishning usullaridan biri - ijobiy dalillar uchun Eyler integralidan foydalanish va takrorlanish formulasini takroran qo'llash orqali domenni salbiy sonlarga etkazish,^[1]

{displaystyle Gamma (z) = {frac {Gamma (z + n + 1)} {z (z + 1) cdots (z + n)}},}

tanlash ${displaystyle n}$ shu kabi ${displaystyle z + n}$ ijobiy. Qachonki maxrajdagi mahsulot nolga teng ${displaystyle z}$ har qanday butun songa teng ${displaystyle 0, -1, -2, cdots}$ . Shunday qilib, gamma funktsiyasini oldini olish uchun ushbu nuqtalarda aniqlanmagan bo'lishi kerak nolga bo'linish; bu a meromorfik funktsiya bilan oddiy qutblar musbat bo'lmagan sonlarda.^[1]

Funktsiya uchun ${displaystyle f}$ murakkab o'zgaruvchining ${displaystyle z}$ , a oddiy qutb ${displaystyle c}$ , qoldiq ning ${displaystyle f}$ tomonidan berilgan:

{displaystyle operator nomi {Res} (f, c) = lim _ {z o c} (z-c) f (z).}

Oddiy qutb uchun ${displaystyle z = -n,}$ takrorlanish formulasini quyidagicha yozamiz:

{displaystyle (z + n) Gamma (z) = {frac {Gamma (z + n + 1)} {z (z + 1) cdots (z + n-1)}}.}

Nomer ${displaystyle z = -n,}$ bu

{displaystyle Gamma (z + n + 1) = Gamma (1) = 1}

va maxraj

{displaystyle z (z + 1) cdots (z + n-1) = - n (1-n) cdots (n-1-n) = (- 1) ^ {n} n !.}

Shunday qilib, gamma funktsiyasining ushbu nuqtalardagi qoldiqlari:

{displaystyle operator nomi {Res} (Gamma, -n) = {frac {(-1) ^ {n}} {n!}}.}

^[8]

Gamma funktsiyasi haqiqiy chiziq bo'ylab hamma joyda nolga teng emas, garchi u o'zboshimchalik bilan nolga yaqin bo'lsa $z \to -\infty$ . Aslida murakkab raqam yo'q ${displaystyle z}$ buning uchun ${displaystyle Gamma (z) = 0}$ va shuning uchun o'zaro gamma funktsiyasi ${extstyle {frac {1} {Gamma (z)}}}$ bu butun funktsiya, nol bilan ${displaystyle z = 0, -1, -2, cdots}$ .^[1]

Minima

Gamma funktsiyasi mahalliy minimal darajaga ega $z min \approx +1.46163 214496836234126$ (qisqartirilgan) qiymatga erishadigan joyda $Γ (z min) \approx +0.88560 319441088870027$ (qisqartirilgan). Gamma funktsiyasi qutblar orasidagi o'zgaruvchan belgi bo'lishi kerak, chunki oldinga qaytishdagi mahsulot toq sonli salbiy omillarni o'z ichiga oladi, agar orasidagi qutblar soni ${displaystyle z}$ va ${displaystyle z + n}$ toq, qutblar soni juft bo'lsa, juft son.^[8]

Integral vakolatxonalar

Ikkinchi turdagi Eyler integralidan tashqari, gamma funktsiyasini integral sifatida ifodalovchi ko'plab formulalar mavjud. Masalan, qachon haqiqiy qismi $z$ ijobiy,^[9]

{displaystyle Gamma (z) = int _ {0} ^ {1} chap (log {frac {1} {t}} ight) ^ {z-1}, dt.}

Gamening funktsiyasi uchun Binetning birinchi integral formulasi, qachonki uning haqiqiy qismi $z$ ijobiy, keyin:^[10]

{displaystyle log Gamma (z) = chap (z- {frac {1} {2}} ight) log z-z + {frac {1} {2}} log (2pi) + int _ {0} ^ {infty} chap ({frac {1} {2}} - {frac {1} {t}} + {frac {1} {e ^ {t} -1}} ight) {frac {e ^ {- tz}} { t}}, dt.}

O'ng tarafdagi integralni a deb talqin qilish mumkin Laplasning o'zgarishi. Anavi,

{displaystyle log chap (Gamma (z) chap ({frac {e} {z}} ight) ^ {z} {sqrt {2pi z}} ight) = {mathcal {L}} chap ({frac {1} {) 2t}} - {frac {1} {t ^ {2}}} + {frac {1} {t (e ^ {t} -1)}} ight) (z).}

Binetning ikkinchi integral formulasi, yana qachon haqiqiy qismi $z$ ijobiy, keyin:^[11]

{displaystyle log Gamma (z) = chap (z- {frac {1} {2}} ight) log z-z + {frac {1} {2}} log (2pi) + 2int _ {0} ^ {infty} {frac {arctan (t / z)} {e ^ {2pi t} -1}}, dt.}

Ruxsat bering $C$ bo'lishi a Hankel konturi, nuqtada boshlanadigan va tugaydigan yo'lni anglatadi $\infty$ ustida Riman shar, uning birlik teginish vektori yaqinlashadi $-1$ yo'lning boshida va $1$ oxirida, u bor o'rash raqami 1 atrofida $0$ va qaysi biri kesib o'tmaydi $[0, \infty)$ . Ning filialini tuzatish ${displaystyle log (-t)}$ bo'ylab kesilgan filialni olib $[0, \infty)$ va qabul qilish orqali ${displaystyle log (-t)}$ qachon haqiqiy bo'lish $t$ manfiy real o'qida joylashgan. Faraz qiling $z$ butun son emas. Keyin gamma funktsiyasi uchun Hankel formulasi:^[12]

{displaystyle Gamma (z) = - {frac {1} {2isin pi z}} int _ {C} (- t) ^ {z-1} e ^ {- t}, dt,}

qayerda ${displaystyle (-t) ^ {z-1}}$ deb talqin etiladi ${displaystyle exp ((z-1) log (-t))}$ . Ko'zgu formulasi bir-biriga chambarchas bog'liq bo'lgan ifodaga olib keladi

{displaystyle {frac {1} {Gamma (z)}} = {frac {i} {2pi}} int _ {C} (- t) ^ {- z} e ^ {- t}, dt,}

har doim yana amal qiladi $z$ butun son emas.

Fourier seriyasining kengayishi

The gamma funktsiyasining logarifmi quyidagilarga ega Fourier seriyasi uchun kengaytirish ${displaystyle 0$

{displaystyle ln Gamma (z) = chap ({frac {1} {2}} - zight) (gamma + ln 2) + (1-z) ln pi - {frac {1} {2}} ln sin (pi z) + {frac {1} {pi}} sum _ {n = 1} ^ {infty} {frac {ln n} {n}} sin (2pi nz),}

uzoq vaqtdan beri bog'liq bo'lgan Ernst Kummer, uni 1847 yilda kim chiqargan.^[13]^[14] Biroq, Yaroslav Blaguchin buni aniqladi Karl Yoxan Malmsten birinchi bo'lib ushbu seriyani 1842 yilda chiqargan.^[15]^[16]

Raabening formulasi

1840 yilda Jozef Lyudvig Raabe buni isbotladi

{displaystyle int _ {a} ^ {a + 1} ln Gamma (z), dz = {frac {1} {2}} ln 2pi + aln a-a, quad a> 0.}

Xususan, agar ${displaystyle a = 0}$ keyin

{displaystyle int _ {0} ^ {1} ln Gamma (z), dz = {frac {1} {2}} ln 2pi.}

Ikkinchisini yuqoridagi ko'paytma formulasida logarifma asosida olish mumkin, bu integralning Riman summasi uchun ifoda beradi. Cheklovni olish ${displaystyle aightarrow infty}$ formulasini beradi.

Pi funktsiyasi

Dastlab kiritilgan muqobil yozuv Gauss va ba'zan ishlatilgan ${displaystyle Pi}$ -funktsiya, bu gamma funktsiyasi nuqtai nazaridan

{displaystyle Pi (z) = Gamma (z + 1) = zGamma (z) = int _ {0} ^ {infty} e ^ {- t} t ^ {z}, dt,}

Shuning uchun; ... uchun; ... natijasida ${displaystyle Pi (n) = n!}$ har qanday salbiy bo'lmagan butun son uchun ${displaystyle n}$ .

Pi funktsiyasidan foydalangan holda aks ettirish formulasi shaklni oladi

{displaystyle Pi (z) Pi (-z) = {frac {pi z} {sin (pi z)}} = {frac {1} {operatorname {sinc} (z)}}}

qayerda $samimiy$ normallashtirilgan sinc funktsiyasi, ko'payish teoremasi shaklni oladi

{displaystyle Pi chap ({frac {z} {m}} ight), Pi chap ({frac {z-1} {m}} ight) cdots Pi chap ({frac {z-m + 1} {m}} ight) = (2pi) ^ {frac {m-1} {2}} m ^ {- z- {frac {1} {2}}} Pi (z).}

Ba'zida biz ham topamiz

{displaystyle pi (z) = {frac {1} {Pi (z)}},}

qaysi bir butun funktsiya kabi har bir murakkab son uchun aniqlangan o'zaro gamma funktsiyasi. Bu ${displaystyle pi (z)}$ Umuman olganda uning qutblari yo'q, shuning uchun ${displaystyle Pi chapda (zight)}$ , kabi ${displaystyle Gamma chap (zight)}$ , yo'q nollar.

The hajmi $n$ -ellipsoid radius bilan $r 1, ..., r n$ sifatida ifodalanishi mumkin

{displaystyle V_ {n} (r_ {1}, dotsc, r_ {n}) = {frac {pi ^ {frac {n} {2}}} {Pi chap ({frac {n} {2}} ight) }} prod _ {k = 1} ^ {n} r_ {k}.}

Boshqa funktsiyalar bilan bog'liqlik

Yuqoridagi gamma funktsiyani belgilaydigan birinchi integralda integratsiya chegaralari aniqlangan. Yuqori va pastki to'liq bo'lmagan gamma funktsiyalari integratsiyaning pastki yoki yuqori (mos ravishda) chegarasi o'zgarishiga imkon berish orqali olingan funktsiyalardir.
Gamma funktsiyasi bilan bog'liq beta funktsiyasi formula bo'yicha

{displaystyle mathrm {B} (x, y) = int _ {0} ^ {1} t ^ {x-1} (1-t) ^ {y-1}, dt = {frac {Gamma (x), Gamma (y)} {Gamma (x + y)}}.}

The logaritmik lotin gamma funktsiyasining digamma funktsiyasi; yuqori hosilalar bu poligamma funktsiyalari.
A bo'yicha gamma funktsiyasining analogi cheklangan maydon yoki a cheklangan halqa bo'ladi Gauss summalari, turi eksponent sum.
The o'zaro gamma funktsiyasi bu butun funktsiya va ma'lum bir mavzu sifatida o'rganilgan.
Gamma funktsiyasi ham bilan muhim aloqada namoyon bo'ladi Riemann zeta funktsiyasi, ${displaystyle zeta (z)}$ .

{displaystyle pi ^ {- {frac {z} {2}}}; Gamma chap ({frac {z} {2}} ight) zeta (z) = pi ^ {- {frac {1-z} {2} }}; Gamma chapda ({frac {1-z} {2}} tun); zeta (1-z).}

Shuningdek, u quyidagi formulada ko'rinadi:

{displaystyle zeta (z) Gamma (z) = int _ {0} ^ {infty} {frac {u ^ {z}} {e ^ {u} -1}}, {frac {du} {u}}, }

faqat uchun amal qiladi

{displaystyle Re (z)> 1}

.

Gamma funktsiyasining logarifmi Lerch tufayli quyidagi formulani qondiradi:

{displaystyle log Gamma (x) = zeta _ {H} '(0, x) -zeta' (0),}

qayerda

{displaystyle zeta _ {H}}

bo'ladi Hurwitz zeta funktsiyasi,

{displaystyle zeta}

Riemann zeta funktsiyasi va asosiy (

'

) birinchi o'zgaruvchida farqlanishni bildiradi.

Gamma funktsiyasi bilan bog'liq kengaytirilgan eksponent funktsiya. Masalan, ushbu funktsiyaning momentlari

{displaystyle langle au ^ {n} angle equiv int _ {0} ^ {infty} dt, t ^ {n-1}, e ^ {- left ({frac {t} {au}} ight) ^ {eta} } = {frac {au ^ {n}} {eta}} Gamma qoldi ({n over eta} ight).}

Maxsus qiymatlar

O'nli kasrdan keyingi dastlabki 20 ta raqamni o'z ichiga olgan holda, gamma funktsiyasining ba'zi bir alohida qiymatlari:

{displaystyle {egin {array} {rcccl} Gamma chapda (- {frac {3} {2}} ight) & = & {frac {4} {3}} {sqrt {pi}} & approx & + 2.36327,18012, 07354,70306 Gamma chap (- {frac {1} {2}} ight) & = & - 2 {sqrt {pi}} & approx & -3,54490,77018,11032,05459 Gamma chap ({frac {1} {) 2}} ight) & = & {sqrt {pi}} & approx & + 1.77245,38509,05516,02729 Gamma (1) & = & 0! & = & + 1 Gamma qoldi ({frac {3} {2}) } ight) & = & {frac {1} {2}} {sqrt {pi}} & approx & + 0.88622,69254,52758,01364 Gamma (2) & = & 1! & = & + 1 Gamma qoldi ({ frac {5} {2}} ight) & = & {frac {3} {4}} {sqrt {pi}} & approx & + 1.32934,03881,79137,02047 Gamma (3) & = & 2! & = & +2 Gamma chapda ({frac {7} {2}} ight) & = & {frac {15} {8}} {sqrt {pi}} & approx & + 3.32335,09704,47842,55118 Gamma (4) & = & 3! & = & + 6end {array}}}

Murakkab qiymatli gamma funktsiyasi musbat bo'lmagan tamsayılar uchun aniqlanmagan, ammo bu holatlarda qiymatni Riman shar kabi $\infty$ . The o'zaro gamma funktsiyasi bu yaxshi belgilangan va analitik ushbu qiymatlarda (va butun murakkab tekislik ):

{displaystyle {frac {1} {Gamma (-3)}} = {frac {1} {Gamma (-2)}} = {frac {1} {Gamma (-1)}} = {frac {1} { Gamma (0)}} = 0.}

Log-gamma funktsiyasi

Analitik funktsiya

jurnal Γ (z)

O'rtacha katta argumentlar uchun gamma va faktorial funktsiyalar juda tez o'sib borganligi sababli, ko'plab hisoblash muhitlari funktsiyani o'z ichiga oladi tabiiy logaritma gamma funktsiyasining (ko'pincha nom beriladi) lgamma yoki lngamma dasturlash muhitida yoki gammaln elektron jadvallarda); bu juda sekin o'sib boradi va kombinatoriya hisob-kitoblari uchun juda katta qiymatlarni ko'paytirish va bo'lish o'rniga jurnallarni qo'shish va olib tashlashga imkon beradi. Bu ko'pincha aniqlanadi^[17]

{displaystyle ln Gamma (z) = - gamma z-ln z + sum _ {k = 1} ^ {infty} left [{frac {z} {k}} - ln left (1+ {frac {z} {k }} yaxshi)

The digamma funktsiyasi, bu funktsiyaning lotinidir, odatda ham ko'rinadi.Texnik va fizikaviy qo'llanmalar sharoitida, masalan. to'lqin tarqalishi bilan, funktsional tenglama

{displaystyle ln Gamma (z) = ln Gamma (z + 1) -ln z}

ko'pincha ishlatiladi, chunki u 1 dyuymli kenglikdagi funktsiya qiymatlarini aniqlashga imkon beradi $z$ qo'shni chiziqdan. Xususan, a uchun yaxshi taxmin bilan boshlang $z$ katta real qism bilan kerakli bosqichga bosqichma-bosqich o'tish mumkin $z$ . Ko'rsatkichidan so'ng Karl Fridrix Gauss, Rocktaeschel (1922) uchun taklif qilingan ${displaystyle ln (Gamma (z))}$ katta uchun taxminiy $Qayta (z)$ :

{displaystyle ln Gamma (z) taxminan (z- {frac {1} {2}}) ln z-z + {frac {1} {2}} ln (2pi)}

Bu aniq taxmin qilish uchun ishlatilishi mumkin $ln (Γ (z))$ uchun $z$ kichikroq bilan $Qayta (z)$ orqali (P.E.Bohmer, 1939)

{displaystyle ln Gamma (z-m) = ln Gamma (z) -sum _ {k = 1} ^ {m} ln (z-k).}

Asimptotik kengayishdan ko'proq atamalar yordamida aniqroq taxminiy natijani olish mumkin $ln (Γ (z))$ va $Γ (z)$ , ular Stirlingning yaqinlashishiga asoslangan.

{displaystyle Gamma (z) sim z ^ {z- {frac {1} {2}}} e ^ {- z} {sqrt {2pi}} chap (1+ {frac {1} {12z}} + {frac {1} {288z ^ {2}}} - {frac {139} {51,840z ^ {3}}} - {frac {571} {2,488,320z ^ {4}}} tunda)}

kabi

| z | \to \infty

doimiy ravishda

| arg (z) | <π

.

Keyinchalik "tabiiy" taqdimotda:

{displaystyle ln Gamma (z) sim zln (z) -z- {frac {1} {2}} ln chap ({frac {z} {2pi}} ight) + {frac {1} {12z}} - { frac {1} {360z ^ {3}}} + {frac {1} {1260z ^ {5}}}}

kabi

| z | \to \infty

doimiy ravishda

| arg (z) | <π

.

Bilan atamalarning koeffitsientlari $k > 1$ ning $z - k + 1$ oxirgi kengayishda oddiygina

{displaystyle {frac {B_ {k}} {k (k-1)}}}

qaerda $B k$ ular Bernulli raqamlari.

Xususiyatlari

The Bor-Mollerup teoremasi faktorial funktsiyalarni musbat real sonlarga kengaytiradigan barcha funktsiyalar orasida faqat gamma funktsiya mavjudligini ta'kidlaydi qavariq, ya'ni uning tabiiy logaritma bu qavariq ijobiy real o'qda. Yana bir tavsif Vilandt teoremasi.

Muayyan ma'noda $ln (Γ)$ funktsiya tabiiyroq shakl; bu funktsiyalarning ba'zi ichki xususiyatlarini aniqroq qiladi. Ajoyib misol Teylor seriyasi ning $ln (Γ)$ 1 atrofida:

{displaystyle ln Gamma (z + 1) = - gamma z + sum _ {k = 2} ^ {infty} {frac {zeta (k)} {k}}, (- z) ^ {k} qquad forall; | z | <1}

bilan $ζ (k)$ belgilaydigan Riemann zeta funktsiyasi da $k$ .

Shunday qilib, quyidagi xususiyatdan foydalaning:

{displaystyle zeta (s) Gamma (s) = int _ {0} ^ {infty} {frac {t ^ {s}} {e ^ {t} -1}}, {frac {dt} {t}}}

uchun integral tasvirni topishimiz mumkin $ln (Γ)$ funktsiyasi:

{displaystyle ln Gamma (z + 1) = - gamma z + int _ {0} ^ {infty} {frac {, chap (e ^ {- zt} -1 + ztight),} {tleft (e ^ {t} -1 tun)}}, dt}

yoki sozlash $z = 1$ uchun integralni olish $γ$ , biz o'rnini bosa olamiz $γ$ termini uning integrali bilan va yuqoridagi formulaga kiriting:

{displaystyle ln Gamma (z + 1) = int _ {0} ^ {infty} {frac {, chap (e ^ {- zt} -ze ^ {- t} -1 + zight),} {t (e ^ {t} -1)}}, dt ,.}

Ratsionallik uchun gamma funktsiyasi logarifmi uchun maxsus formulalar ham mavjud $z$ . Masalan, agar ${displaystyle k}$ va ${displaystyle n}$ bilan butun sonlar mavjud ${displaystyle k$ va ${displaystyle keq n / 2 ,,}$ keyin

{displaystyle {egin {aligned} ln Gamma {iggl (}! {frac {k} {n}}! {iggr)} = {} & {frac {, (n-2k) ln 2pi,} {2n}} + {frac {1} {2}} chap {, ln pi -ln sin {frac {pi k} {n}}, ight} + {frac {1} {pi}}! sum _ {r = 1} ^ { n-1} {frac {, gamma + ln r,} {r}} cdot sin {frac {, 2pi rk,} {n}} & {} - {frac {1} {2pi}} sin {frac { 2pi k} {n}} cdot! Int _ {0} ^ {infty} !! {frac {, e ^ {- nx}! Cdot ln x,} {, cosh x-cos (2pi k / n),} }, {mathrm {d}} xend {aligned}}}

qarang.^[18]Ushbu formuladan ba'zida raqamli hisoblash uchun foydalaniladi, chunki integral juda tez pasayadi.

Log-gamma bo'yicha integratsiya

Integral

{displaystyle int _ {0} ^ {z} ln Gamma (x), dx}

bilan ifodalanishi mumkin Barns $G$ -funktsiya^[19]^[20] (qarang Barns $G$ -funktsiya dalil uchun):

{displaystyle int _ {0} ^ {z} ln Gamma (x), dx = {frac {z} {2}} ln (2pi) + {frac {z (1-z)} {2}} + zln Gamma (z) -ln G (z + 1)}

qayerda $Qayta (z) > -1$ .

Shuningdek, so'zlari bilan yozilishi mumkin Hurwitz zeta funktsiyasi:^[21]^[22]

{displaystyle int _ {0} ^ {z} ln Gamma (x), dx = {frac {z} {2}} ln (2pi) + {frac {z (1-z)} {2}} - zeta ' (-1) + zeta '(-1, z).}

Qachon ${displaystyle z = 1}$ bundan kelib chiqadiki

{displaystyle int _ {0} ^ {1} ln Gamma (x), dx = {frac {1} {2}} log (2pi),}

va bu natijadir Raabening formulasi shuningdek. O. Espinosa va V. Moll ning kvadratining integralining o'xshash formulasini olishdi ${displaystyle log Gamma}$ :^[23]

{displaystyle int _ {0} ^ {1} log ^ {2} Gamma (x) dx = {frac {gamma ^ {2}} {12}} + {frac {pi ^ {2}} {48}} + {frac {1} {3}} gamma L_ {1} + {frac {4} {3}} L_ {1} ^ {2} -chap (gamma + 2L_ {1} tun) {frac {zeta ^ {prime } (2)} {pi ^ {2}}} + {frac {zeta ^ {prime prime} (2)} {2pi ^ {2}}},}

qayerda ${displaystyle L_ {1}}$ bu ${displaystyle {frac {1} {2}} log (2pi)}$ .

D. H. Beyli va uning hammualliflari^[24] uchun baho berdi

{displaystyle L_ {n}: = int _ {0} ^ {1} log ^ {n} Gamma (x) dx}

qachon ${displaystyle n = 1,2}$ Tornxaym-Vitten zeta funktsiyasi va uning hosilalari nuqtai nazaridan.

Bundan tashqari, bu ham ma'lum^[25]

{displaystyle lim _ {n o infty} {frac {L_ {n}} {n!}} = 1.}

Yaqinlashishlar

Comparison gamma (blue line) with the factorial (blue dots) and Stirling's approximation (red line)

Complex values of the gamma function can be computed numerically with arbitrary precision using Stirlingning taxminiy qiymati yoki Lanczos approximation.

The gamma function can be computed to fixed precision for ${displaystyle operatorname {Re} (z)in [1,2]}$ by applying qismlar bo'yicha integratsiya to Euler's integral. For any positive number $x$ the gamma function can be written

{displaystyle { egin{aligned}Gamma (z)&=int _{0}^{x}e^{-t}t^{z},{frac {dt}{t}}+int _{x}^{infty }e^{-t}t^{z},{frac {dt}{t}}&=x^{z}e^{-x}sum _{n=0}^{infty }{frac {x^{n}}{z(z+1)cdots (z+n)}}+int _{x}^{infty }e^{-t}t^{z},{frac {dt}{t}}.end{aligned}}}

Qachon $Qayta (z) \in [1,2]$ va ${displaystyle xgeq 1}$ , the absolute value of the last integral is smaller than ${displaystyle (x+1)e^{-x}}$ . By choosing a large enough ${displaystyle x}$ , this last expression can be made smaller than ${displaystyle 2^{-N}}$ for any desired value ${displaystyle N}$ . Thus, the gamma function can be evaluated to ${displaystyle N}$ bits of precision with the above series.

A fast algorithm for calculation of the Euler gamma function for any algebraic argument (including rational) was constructed by E.A. Karatsuba,^[26]^[27]^[28]

For arguments that are integer multiples of $1 / 24$ , the gamma function can also be evaluated quickly using o'rtacha arifmetik - geometrik o'rtacha iterations (see particular values of the gamma function va Borwein & Zucker (1992)).

Ilovalar

One author describes the gamma function as "Arguably, the most common special function, or the least 'special' of them. The other transcendental functions […] are called 'special' because you could conceivably avoid some of them by staying away from many specialized mathematical topics. On the other hand, the gamma function $y = Γ(x)$ is most difficult to avoid."^[29]

Integration problems

The gamma function finds application in such diverse areas as kvant fizikasi, astrofizika va suyuqlik dinamikasi.^[30] The gamma distribution, which is formulated in terms of the gamma function, is used in statistika to model a wide range of processes; for example, the time between occurrences of earthquakes.^[31]

The primary reason for the gamma function's usefulness in such contexts is the prevalence of expressions of the type ${displaystyle f(t)e^{-g(t)}}$ which describe processes that decay exponentially in time or space. Integrals of such expressions can occasionally be solved in terms of the gamma function when no elementary solution exists. Masalan, agar $f$ is a power function and $g$ is a linear function, a simple change of variables gives the evaluation

{displaystyle int _{0}^{infty }t^{b}e^{-at},dt={frac {Gamma (b+1)}{a^{b+1}}}.}

The fact that the integration is performed along the entire positive real line might signify that the gamma function describes the cumulation of a time-dependent process that continues indefinitely, or the value might be the total of a distribution in an infinite space.

It is of course frequently useful to take limits of integration other than 0 and $\infty$ to describe the cumulation of a finite process, in which case the ordinary gamma function is no longer a solution; the solution is then called an to'liq bo'lmagan gamma funktsiyasi. (The ordinary gamma function, obtained by integrating across the entire positive real line, is sometimes called the complete gamma function for contrast.)

An important category of exponentially decaying functions is that of Gauss funktsiyalari

{displaystyle ae^{-{frac {(x-b)^{2}}{c^{2}}}}}

and integrals thereof, such as the xato funktsiyasi. There are many interrelations between these functions and the gamma function; notably, the factor ${displaystyle {sqrt {pi }}}$ obtained by evaluating ${ extstyle Gamma left({frac {1}{2}}ight)}$ is the "same" as that found in the normalizing factor of the error function and the normal taqsimot.

The integrals we have discussed so far involve transcendental functions, but the gamma function also arises from integrals of purely algebraic functions. Xususan, arc lengths ning ellipslar va lemniscate, which are curves defined by algebraic equations, are given by elliptik integrallar that in special cases can be evaluated in terms of the gamma function. The gamma function can also be used to calculate "volume" and "area" ning $n$ - o'lchovli giperferalar.

Calculating products

The gamma function's ability to generalize factorial products immediately leads to applications in many areas of mathematics; yilda kombinatorika, and by extension in areas such as ehtimollik nazariyasi va hisoblash quvvat seriyasi. Many expressions involving products of successive integers can be written as some combination of factorials, the most important example perhaps being that of the binomial koeffitsient

{displaystyle {inom {n} {k}} = {frac {n!} {k! (n-k)!}}.}

The example of binomial coefficients motivates why the properties of the gamma function when extended to negative numbers are natural. A binomial coefficient gives the number of ways to choose $k$ to'plamidan elementlar $n$ elementlar; agar $k > n$ , there are of course no ways. Agar $k > n$ , $(n - k)!$ is the factorial of a negative integer and hence infinite if we use the gamma function definition of factorials—dividing by infinity gives the expected value of 0.

We can replace the factorial by a gamma function to extend any such formula to the complex numbers. Generally, this works for any product wherein each factor is a ratsional funktsiya of the index variable, by factoring the rational function into linear expressions. Agar $P$ va $Q$ are monic polynomials of degree $m$ va $n$ with respective roots $p 1, \dots, p m$ va $q 1, \dots, q n$ , bizda ... bor

{displaystyle prod _{i=a}^{b}{frac {P(i)}{Q(i)}}=left(prod _{j=1}^{m}{frac {Gamma (b-p_{j}+1)}{Gamma (a-p_{j})}}ight)left(prod _{k=1}^{n}{frac {Gamma (a-q_{k})}{Gamma (b-q_{k}+1)}}ight).}

If we have a way to calculate the gamma function numerically, it is a breeze to calculate numerical values of such products. The number of gamma functions in the right-hand side depends only on the degree of the polynomials, so it does not matter whether $b - a$ equals 5 or 10⁵. By taking the appropriate limits, the equation can also be made to hold even when the left-hand product contains zeros or poles.

By taking limits, certain rational products with infinitely many factors can be evaluated in terms of the gamma function as well. Tufayli Vaystrasht faktorizatsiya teoremasi, analytic functions can be written as infinite products, and these can sometimes be represented as finite products or quotients of the gamma function. We have already seen one striking example: the reflection formula essentially represents the sine function as the product of two gamma functions. Starting from this formula, the exponential function as well as all the trigonometric and hyperbolic functions can be expressed in terms of the gamma function.

More functions yet, including the hypergeometric function and special cases thereof, can be represented by means of complex kontur integrallari of products and quotients of the gamma function, called Mellin–Barnes integrals.

Analitik sonlar nazariyasi

An elegant and deep application of the gamma function is in the study of the Riemann zeta funktsiyasi. A fundamental property of the Riemann zeta function is its funktsional tenglama:

{displaystyle Gamma left({frac {s}{2}}ight)zeta (s)pi ^{-{frac {s}{2}}}=Gamma left({frac {1-s}{2}}ight)zeta (1-s)pi ^{-{frac {1-s}{2}}}.}

Among other things, this provides an explicit form for the analitik davomi of the zeta function to a meromorphic function in the complex plane and leads to an immediate proof that the zeta function has infinitely many so-called "trivial" zeros on the real line. Borwein va boshq. call this formula "one of the most beautiful findings in mathematics".^[32] Another champion for that title might be

{displaystyle zeta (s);Gamma (s)=int _{0}^{infty }{frac {t^{s}}{e^{t}-1}},{frac {dt}{t}}.}

Both formulas were derived by Bernxard Riman in his seminal 1859 paper "Über die Anzahl der Primzahlen unter einer gegebenen Größe" ("On the Number of Prime Numbers less than a Given Quantity"), one of the milestones in the development of analitik sonlar nazariyasi —the branch of mathematics that studies tub sonlar using the tools of mathematical analysis. Factorial numbers, considered as discrete objects, are an important concept in classical number theory because they contain many prime factors, but Riemann found a use for their continuous extension that arguably turned out to be even more important.

Tarix

The gamma function has caught the interest of some of the most prominent mathematicians of all time. Its history, notably documented by Filipp J. Devis in an article that won him the 1963 Chauvenet mukofoti, reflects many of the major developments within mathematics since the 18th century. In the words of Davis, "each generation has found something of interest to say about the gamma function. Perhaps the next generation will also."^[1]

18th century: Euler and Stirling

Daniel Bernulli ga xat Christian Goldbach, October 6, 1729

The problem of extending the factorial to non-integer arguments was apparently first considered by Daniel Bernulli va Christian Goldbach in the 1720s, and was solved at the end of the same decade by Leonhard Eyler. Euler gave two different definitions: the first was not his integral but an cheksiz mahsulot,

{displaystyle n!=prod _{k=1}^{infty }{frac {left(1+{frac {1}{k}}ight)^{n}}{1+{frac {n}{k}}}},,}

of which he informed Goldbach in a letter dated October 13, 1729. He wrote to Goldbach again on January 8, 1730, to announce his discovery of the integral representation

{displaystyle n!=int _{0}^{1}(-ln s)^{n},ds,,}

which is valid for $n > 0$ . By the change of variables $t = -ln s$ , this becomes the familiar Euler integral. Euler published his results in the paper "De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt" ("On transcendental progressions, that is, those whose general terms cannot be given algebraically"), submitted to the Sankt-Peterburg akademiyasi on November 28, 1729.^[33] Euler further discovered some of the gamma function's important functional properties, including the reflection formula.

Jeyms Stirling, a contemporary of Euler, also attempted to find a continuous expression for the factorial and came up with what is now known as Stirling formulasi. Although Stirling's formula gives a good estimate of $n!$ , also for non-integers, it does not provide the exact value. Extensions of his formula that correct the error were given by Stirling himself and by Jak Filipp Mari Binet.

19th century: Gauss, Weierstrass and Legendre

The first page of Euler's paper

Karl Fridrix Gauss rewrote Euler's product as

{displaystyle Gamma (z)=lim _{m o infty }{frac {m^{z}m!}{z(z+1)(z+2)cdots (z+m)}}}

and used this formula to discover new properties of the gamma function. Although Euler was a pioneer in the theory of complex variables, he does not appear to have considered the factorial of a complex number, as instead Gauss first did.^[34] Gauss also proved the ko'paytirish teoremasi of the gamma function and investigated the connection between the gamma function and elliptik integrallar.

Karl Vaystrass further established the role of the gamma function in kompleks tahlil, starting from yet another product representation,

{displaystyle Gamma (z)={frac {e^{-gamma z}}{z}}prod _{k=1}^{infty }left(1+{frac {z}{k}}ight)^{-1}e^{frac {z}{k}},}

qayerda $γ$ bo'ladi Eyler-Maskeroni doimiysi. Weierstrass originally wrote his product as one for $1 / Γ$ , in which case it is taken over the function's zeros rather than its poles. Inspired by this result, he proved what is known as the Vaystrasht faktorizatsiya teoremasi —that any entire function can be written as a product over its zeros in the complex plane; a generalization of the algebraning asosiy teoremasi.

The name gamma function and the symbol $Γ$ tomonidan kiritilgan Adrien-Mari Legendre around 1811; Legendre also rewrote Euler's integral definition in its modern form. Although the symbol is an upper-case Greek gamma, there is no accepted standard for whether the function name should be written "gamma function" or "Gamma function" (some authors simply write " $Γ$ -function"). The alternative "pi function" notation $Π (z) = z!$ due to Gauss is sometimes encountered in older literature, but Legendre's notation is dominant in modern works.

It is justified to ask why we distinguish between the "ordinary factorial" and the gamma function by using distinct symbols, and particularly why the gamma function should be normalized to $Γ (n + 1) = n!$ instead of simply using " $Γ (n) = n!$ ". Consider that the notation for exponents, $x n$ , has been generalized from integers to complex numbers $x z$ without any change. Legendre's motivation for the normalization does not appear to be known, and has been criticized as cumbersome by some (the 20th-century mathematician Kornelius Lancos, for example, called it "void of any rationality" and would instead use $z!$ ).^[35] Legendre's normalization does simplify a few formulae, but complicates most others. From a modern point of view, the Legendre normalization of the Gamma function is the integral of the additive belgi $e - x$ against the multiplicative character $x z$ ga nisbatan Haar o'lchovi ${displaystyle { frac {dx}{x}}}$ ustida Yolg'on guruh $R +$ . Thus this normalization makes it clearer that the gamma function is a continuous analogue of a Gauss summasi.

19th–20th centuries: characterizing the gamma function

It is somewhat problematic that a large number of definitions have been given for the gamma function. Garchi ular bir xil funktsiyani tavsiflasalar ham, ekvivalentlikni isbotlash umuman to'g'ri emas. Stirling uning kengaytirilgan formulasi Eylerning gamma funktsiyasiga to'liq mos kelishini hech qachon isbotlamagan; birinchi marta dalil keltirildi Charlz Hermit 1900 yilda.^[36] Har bir formulaga ixtisoslashgan dalil topish o'rniga, gamma funktsiyani aniqlashning umumiy uslubiga ega bo'lish maqsadga muvofiqdir.

Isbotlashning usullaridan biri a ni topishdir differentsial tenglama gamma funktsiyasini tavsiflovchi. Amaliy matematikadagi aksariyat maxsus funktsiyalar echimlari noyob bo'lgan differentsial tenglamalar echimlari sifatida paydo bo'ladi. Biroq, gamma funktsiyasi hech qanday oddiy differentsial tenglamani qondirmaydigan ko'rinadi. Otto Xolder gamma funktsiyasi hech bo'lmaganda hech birini qondirmasligini 1887 yilda isbotladi algebraik differentsial tenglama bunday tenglamani echish gamma funktsiyasining takrorlanish formulasini qondira olmasligini ko'rsatib, uni a transandantal transsendental funktsiya. Ushbu natija sifatida tanilgan Xolder teoremasi.

Gamma funktsiyasining aniq va umuman qo'llaniladigan tavsifi 1922 yilgacha berilmagan. Xarald Bor va Yoxannes Mollerup keyin ma'lum bo'lgan narsani isbotladi Bor-Mollerup teoremasi: gamma funktsiyasi faktoriy takrorlanish munosabatlarining yagona ijobiy echimi bo'lib, ijobiy va logaritmik konveks ijobiy uchun $z$ va uning qiymati 1 ga teng bo'lgan 1 (funktsiya logaritmik qavariq bo'lsa, uning logaritmasi qavariq bo'lsa). Yana bir tavsif Vilandt teoremasi.

Bor-Mollerup teoremasi foydalidir, chunki gamma funktsiyasini aniqlash uchun foydalaniladigan har xil formulalar uchun logaritmik konveksiyani isbotlash nisbatan oson. Gamma funktsiyani har qanday ma'lum bir formula bilan belgilash o'rniga, biz Bor-Mollerup teoremasining shartlarini ta'rif sifatida tanlashimiz mumkin, keyin esa gamma funktsiyasini o'rganish uchun boshlang'ich nuqta sifatida biz qondiradigan har qanday formulani tanlashimiz mumkin. . Ushbu yondashuv Burbaki guruhi.

Borwein & Corless^[37] gamma funktsiyasi bo'yicha uch asrlik ishlarni ko'rib chiqing.

Yo'naltiruvchi jadvallar va dasturiy ta'minot

Garchi gamma funktsiyasini zamonaviy kompyuter bilan, hattoki programlanadigan cho'ntak kalkulyatori bilan har qanday matematik jihatdan sodda funktsiyalar kabi deyarli osonlikcha hisoblash mumkin bo'lsa-da, bu har doim ham shunday emas edi. 20-asrning o'rtalariga qadar matematiklar qo'lda tayyorlangan jadvallarga tayanar edilar; gamma funktsiyasi bo'yicha, xususan, 1813 yilda Gauss tomonidan hisoblangan jadval va 1825 yilda Legendre tomonidan hisoblangan jadval.

Dan boshlab murakkab gamma funktsiyasining absolyut qiymatining qo'l bilan chizilgan grafigi Yuqori funktsiyalar jadvallari tomonidan Jahnke va Emde [de ].

Gamma funktsiyasining murakkab qiymatlari jadvallari, shuningdek qo'lda chizilgan grafikalar berilgan Yuqori funktsiyalar jadvallari tomonidan Jahnke va Emde [de ], birinchi bo'lib Germaniyada 1909 yilda nashr etilgan Maykl Berri, "murakkab tekislikdagi gamma funktsiyasining qutblarini ko'rsatadigan uch o'lchovli grafikaning J & E nashrida deyarli ikonik maqomga ega bo'ldi."^[38]

Nazariy fizikada murakkab gamma funktsiyasi uchun dasturlar topilgan 1930-yillarga qadar aslida gamma funktsiyasining haqiqiy qiymatlaridan boshqa hech narsaga amaliy ehtiyoj kam bo'lgan. 1950-yillarda elektron kompyuterlar jadvallarni ishlab chiqarish uchun foydalanish imkoniyatiga ega bo'lganligi sababli, talabni qondirish uchun murakkab gamma funktsiyasi uchun bir nechta keng jadvallar, shu jumladan AQShdan o'nli kasrga to'g'ri keladigan jadval nashr etildi. Milliy standartlar byurosi.^[1]

Abramovits va Stegun 1964 yilda nashr etilgandan so'ng, ushbu va boshqa ko'plab maxsus funktsiyalar uchun standart ma'lumotnoma bo'ldi.

Gamma funktsiyasini va uning logaritmasini ikki aniqlikdagi suzuvchi nuqtali tatbiq etish endi ko'plab ilmiy hisoblash dasturlari va maxsus funktsiyalar kutubxonalarida mavjud. TK hal qiluvchi, Matlab, GNU oktavi, va GNU ilmiy kutubxonasi. Gamma funktsiyasi ham qo'shilgan C standart kutubxona (matematik ). O'zboshimchalik bilan aniqlik bilan amalga oshirish ko'p hollarda mavjud kompyuter algebra tizimlari, kabi Matematik va Chinor. PARI / GP, MPFR va MPFUN bepul o'zboshimchalik bilan aniqlik kiritishni o'z ichiga oladi. Ga kiritilgan kalkulyator dasturining ozgina ma'lum bo'lgan xususiyati Android operatsion tizimi fraksiyonel qiymatlarni faktoriy funktsiyaga kirish sifatida qabul qiladi va ekvivalent gamma funktsiya qiymatini qaytaradi. Xuddi shu narsa uchun ham amal qiladi Windows kalkulyatori (ilmiy rejimda).

Shuningdek qarang

Izohlar

^ ^a ^b ^v ^d ^e ^f ^g ^h ^men ^j ^k ^l ^m ⁿ Devis, P. J. (1959). "Leonhard Eylerning ajralmas qismi: Gamma funktsiyasining tarixiy profili". Amerika matematik oyligi. 66 (10): 849–869. doi:10.2307/2309786. JSTOR 2309786. Olingan 3 dekabr 2016.
^ Beals, Richard; Vong, Roderik (2010). Maxsus funktsiyalar: Bitiruvchi matn. Kembrij universiteti matbuoti. p. 28. ISBN 978-1-139-49043-6. 28-betning ko'chirmasi
^ Ross, Kley C. (2013). Diferensial tenglamalar: Matematikaga kirish (tasvirlangan tahrir). Springer Science & Business Media. p. 293. ISBN 978-1-4757-3949-7. G3 ifodasi 293-betda
^ Kingman, J. F. C. (1961). "Ijobiy matritsalarning konveksiya xususiyati". Matematikaning har choraklik jurnali. 12 (1): 283–284. Bibcode:1961QJMat..12..283K. doi:10.1093 / qmath / 12.1.283.
^ Vayshteyn, Erik V. "Bor-Mollerup teoremasi". MathWorld.
^ ^a ^b Askey, R. A.; Roy, R. (2010), "Seriyalarni kengaytirish", yilda Olver, Frank V. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Klark, Charlz V. (tahr.), NIST Matematik funktsiyalar bo'yicha qo'llanma, Kembrij universiteti matbuoti, ISBN 978-0-521-19225-5, JANOB 2723248
^ Valdschmidt, M. (2006). "Davrlarning transendendentsiyasi: san'at holati" (PDF). Sof Appl. Matematika. Kvart. 2 (2): 435–463. doi:10.4310 / pamq.2006.v2.n2.a3.
^ ^a ^b Vayshteyn, Erik V. "Gamma funktsiyasi". MathWorld.
^ Uittaker va Uotson, 12.2 misol 1.
^ Uittaker va Uotson, 12.31.
^ Uittaker va Uotson, 12.32.
^ Uittaker va Uotson, 12.22.
^ Betmen, Garri; Erdélii, Artur (1955). Yuqori transandantal funktsiyalar. McGraw-Hill.
^ Srivastava, X. M.; Choi, J. (2001). Zeta va tegishli funktsiyalar bilan bog'liq seriyalar. Niderlandiya: Kluwer Academic.
^ Blagouchine, Iaroslav V. (2014). "Malmsten integrallarini qayta kashf etish, ularni konturli integratsiya usullari bilan baholash va shu bilan bog'liq ba'zi natijalar". Ramanujan J. 35 (1): 21–110. doi:10.1007 / s11139-013-9528-5.
^ Blagouchine, Iaroslav V. (2016). Malmstenning integrallarini qayta kashf etish, ularni konturli integratsiya usullari bilan baholash va ularga tegishli ba'zi natijalarga "Erratum va qo'shimchalar""". Ramanujan J. 42 (3): 777–781. doi:10.1007 / s11139-015-9763-z.
^ "Log Gamma funktsiyasi". Wolfram MathWorld. Olingan 3 yanvar 2019.
^ Blagouchine, Iaroslav V. (2015). "Ratsional argumentlar va ba'zi bir bog'liq yig'indilarda birinchi umumlashtirilgan Stielts konstantasini yopiq shaklda baholash teoremasi". Raqamlar nazariyasi jurnali. 148: 537–592. arXiv:1401.3724. doi:10.1016 / j.jnt.2014.08.009.
^ Alekseyjevskiy, V. P. (1894). "Über eine Classe von Funktionen, die der Gammafunktion analog sind" [Gamma funktsiyasiga o'xshash funktsiyalar klassi haqida]. Leypsig Vaydmanncshe Buxhandluns. 46: 268–275.
^ Barns, E. W. (1899). "Nazariyasi G-funktsiya ". Kvart. J. Matematik. 31: 264–314.
^ Adamchik, Viktor S. (1998). "Salbiy tartibdagi poligamma funktsiyalari". J. Komput. Qo'llash. Matematika. 100 (2): 191–199. doi:10.1016 / S0377-0427 (98) 00192-7.
^ Gosper, R. V. (1997). " ${displaystyle extstyle int _ {n / 4} ^ {m / 6} log F (z), dz}$ maxsus funktsiyalarda, q-seriyalar va tegishli mavzular ". J. Am. Matematika. Soc. 14.
^ Espinosa, Olivye; Moll, Viktor H. (2002). "Xurvits Zeta funktsiyasining ba'zi integrallari to'g'risida: 1-qism". Ramanujan jurnali. 6: 159–188. doi:10.1023 / A: 1015706300169.
^ Beyli, Devid X.; Borwein, David; Borwein, Jonathan M. (2015). "Eulerian log-gamma integrallari va Tornxaym-Vitten zeta funktsiyalari to'g'risida". Ramanujan jurnali. 36: 43–68. doi:10.1007 / s11139-012-9427-1.
^ Amdeberhan, T .; Kofi, Mark V.; Espinosa, Olivye; Koutschan, Kristof; Manna, Dante V.; Moll, Viktor H. (2011). "Loggamma kuchlarining integrallari". Proc. Amer. Matematika. Soc. 139 (2): 535–545. doi:10.1090 / S0002-9939-2010-10589-0.
^ E.A. Karatsuba, Transandantal funktsiyalarni tezkor baholash. Probl. Inf. Transm. 27-jild, №4, 339–360-betlar (1991).
^ E.A. Karatsuba, Transandantal funktsiyalarni tezkor baholashning yangi usuli to'g'risida. Russ. Matematika. Surv. 46-jild, № 2, 246–247 betlar (1991).
^ E.A. Karatsuba "Tez algoritmlar va FEE usuli ".
^ Michon, G. P. "Trigonometriya va asosiy funktsiyalar Arxivlandi 2010 yil 9-yanvar kuni Orqaga qaytish mashinasi ". Numerika. 2007 yil 5-mayda olingan.
^ Chaudri, M. A. va Zubair, S. M. (2001). Ilovalar bilan to'liq bo'lmagan gamma funktsiyalari klassi to'g'risida. p. 37
^ Rays, J. A. (1995). Matematik statistika va ma'lumotlarni tahlil qilish (Ikkinchi nashr). p. 52-53
^ Borwein, J .; Beyli, D. H. va Girgensohn, R. (2003). Matematika bo'yicha tajriba. A. K. Peters. p. 133. ISBN 978-1-56881-136-9.
^ Eylerning qog'ozi nashr etilgan Commentarii academiae Scientificiarum Petropolitanae 5, 1738, 36-57. Qarang E19 - algebrais dari nequeunt ning transcendentibus seu kvartum termini generallari, asl maqolaning skanerlangan nusxasini o'z ichiga olgan Eyler arxividan.
^ Remmert, R. (2006). Murakkab funktsiyalar nazariyasidagi klassik mavzular. Kay, L. D. Springer tomonidan tarjima qilingan. ISBN 978-0-387-98221-2.
^ Lanczos, C. (1964). "Gamma funktsiyasining aniq yaqinlashuvi". J. SIAM Numer. Anal. Ser. B. 1.
^ Knut, D. E. (1997). Kompyuter dasturlash san'ati, 1-jild (Asosiy algoritmlar). Addison-Uesli.
^ Borwein, Jonathan M.; Corless, Robert M. (2017). "Oylik gamma va faktorial". Amerika matematik oyligi. Amerika matematik assotsiatsiyasi. 125 (5): 400–24. arXiv:1703.05349. Bibcode:2017arXiv170305349B. doi:10.1080/00029890.2018.1420983.
^ Berri, M. (2001 yil aprel). "Nima uchun maxsus funktsiyalar maxsus?". Bugungi kunda fizika.

Ushbu maqola quyidagi materiallarni o'z ichiga oladi Citizenium maqola "Gamma funktsiyasi "ostida litsenziyalangan Creative Commons Attribution-ShareAlike 3.0 Import qilinmagan litsenziyasi lekin ostida emas GFDL.

Qo'shimcha o'qish

Abramovits, Milton; Stegun, Irene A., nashr. (1972). "6-bob". Matematik funktsiyalar uchun formulalar, grafikalar va matematik jadvallar bilan qo'llanma. Nyu-York: Dover.
Andrews, G. E.; Askey, R .; Roy, R. (1999). "1-bob (Gamma va Beta funktsiyalari)". Maxsus funktsiyalar. Nyu-York: Kembrij universiteti matbuoti. ISBN 978-0-521-78988-2.
Artin, Emil (2006). "Gamma funktsiyasi". Rozenda Maykl (tahrir). Emil Artinning ekspozitsiyasi: tanlov. Matematika tarixi. 30. Providence, RI: Amerika Matematik Jamiyati.
Askey, R.; Roy, R. (2010), "Gamma funktsiyasi", yilda Olver, Frank V. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Klark, Charlz V. (tahr.), NIST Matematik funktsiyalar bo'yicha qo'llanma, Kembrij universiteti matbuoti, ISBN 978-0-521-19225-5, JANOB 2723248
Birxof, Jorj D. (1913). "Gamma funktsiyasi to'g'risida eslatma". Buqa. Amer. Matematika. Soc. 20 (1): 1–10. doi:10.1090 / s0002-9904-1913-02429-7. JANOB 1559418.
Böhmer, P. E. (1939). Differenzengleichungen und bestimmte Integrale [Differentsial tenglamalar va aniq integrallar]. "Leyptsig": "Kyler Verlag".
Devis, Filipp J. (1959). "Leonhard Eylerning ajralmas qismi: Gamma funktsiyasining tarixiy profili". Amerika matematik oyligi. 66 (10): 849–869. doi:10.2307/2309786. JSTOR 2309786.
Press, W. H .; Teukolskiy, S. A .; Vetling, V. T.; Flannery, B. P. (2007). "6.1-bo'lim. Gamma funktsiyasi". Raqamli retseptlar: Ilmiy hisoblash san'ati (3-nashr). Nyu-York: Kembrij universiteti matbuoti. ISBN 978-0-521-88068-8.
Roktashel, O. R. (1922). Metoden zur Berechnung der Gammafunktion für komplekses Argument [Murakkab argumentlar uchun gamma funktsiyasini hisoblash usullari]. Drezden: Drezden Texnik universiteti.
Temme, Niko M. (1996). Maxsus funktsiyalar: Matematik fizikaning klassik funktsiyalari bilan tanishish. Nyu-York: John Wiley & Sons. ISBN 978-0-471-11313-3.
Uittaker, E. T.; Vatson, G. N. (1927). Zamonaviy tahlil kursi. Kembrij universiteti matbuoti. ISBN 978-0-521-58807-2.

Tashqi havolalar

Matematik funktsiyalarning NIST raqamli kutubxonasi: Gamma funktsiyasi
Paskal Sebax va Xaver Gourdon. Gamma funktsiyasiga kirish. Yilda PostScript va HTML formatlari.
Uchun C ++ ma'lumotnomasi std :: tgamma
Gamma funktsiyasi bilan bog'liq muammolarning misollarini topish mumkin Exampleproblems.com.
"Gamma funktsiyasi", Matematika entsiklopediyasi, EMS Press, 2001 [1994]
Wolfram gamma funktsiyasini baholovchi (o'zboshimchalik bilan aniqlik)
"Gamma". Wolfram Vazifalar sayti.
N-Sferalar hajmi va Gamma funktsiyasi MathPages-da

[Davis-1] v ^d ^e ^f ^g ^h ^men ^j ^k ^l ^m ⁿ Devis, P. J. (1959). "Leonhard Eylerning ajralmas qismi: Gamma funktsiyasining tarixiy profili". Amerika matematik oyligi. 66 (10): 849–869. doi:10.2307/2309786. JSTOR 2309786. Olingan 3 dekabr 2016.

[2] Beals, Richard; Vong, Roderik (2010). Maxsus funktsiyalar: Bitiruvchi matn. Kembrij universiteti matbuoti. p. 28. ISBN 978-1-139-49043-6. 28-betning ko'chirmasi

[3] Ross, Kley C. (2013). Diferensial tenglamalar: Matematikaga kirish (tasvirlangan tahrir). Springer Science & Business Media. p. 293. ISBN 978-1-4757-3949-7. G3 ifodasi 293-betda

[Kingman1961-4] Kingman, J. F. C. (1961). "Ijobiy matritsalarning konveksiya xususiyati". Matematikaning har choraklik jurnali. 12 (1): 283–284. Bibcode:1961QJMat..12..283K. doi:10.1093 / qmath / 12.1.283.

[5] Vayshteyn, Erik V. "Bor-Mollerup teoremasi". MathWorld.

[ReferenceA-6] Askey, R. A.; Roy, R. (2010), "Seriyalarni kengaytirish", yilda Olver, Frank V. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Klark, Charlz V. (tahr.), NIST Matematik funktsiyalar bo'yicha qo'llanma, Kembrij universiteti matbuoti, ISBN 978-0-521-19225-5, JANOB 2723248

[7] Valdschmidt, M. (2006). "Davrlarning transendendentsiyasi: san'at holati" (PDF). Sof Appl. Matematika. Kvart. 2 (2): 435–463. doi:10.4310 / pamq.2006.v2.n2.a3.

[Mathworld-8] Vayshteyn, Erik V. "Gamma funktsiyasi". MathWorld.

[9] Uittaker va Uotson, 12.2 misol 1.

[10] Uittaker va Uotson, 12.31.

[11] Uittaker va Uotson, 12.32.

[12] Uittaker va Uotson, 12.22.

[13] Betmen, Garri; Erdélii, Artur (1955). Yuqori transandantal funktsiyalar. McGraw-Hill.

[14] Srivastava, X. M.; Choi, J. (2001). Zeta va tegishli funktsiyalar bilan bog'liq seriyalar. Niderlandiya: Kluwer Academic.

[iaroslav_06-15] Blagouchine, Iaroslav V. (2014). "Malmsten integrallarini qayta kashf etish, ularni konturli integratsiya usullari bilan baholash va shu bilan bog'liq ba'zi natijalar". Ramanujan J. 35 (1): 21–110. doi:10.1007 / s11139-013-9528-5.

[iaroslav_06bis-16] Blagouchine, Iaroslav V. (2016). Malmstenning integrallarini qayta kashf etish, ularni konturli integratsiya usullari bilan baholash va ularga tegishli ba'zi natijalarga "Erratum va qo'shimchalar""". Ramanujan J. 42 (3): 777–781. doi:10.1007 / s11139-015-9763-z.

[17] "Log Gamma funktsiyasi". Wolfram MathWorld. Olingan 3 yanvar 2019.

[iaroslav_07-18] Blagouchine, Iaroslav V. (2015). "Ratsional argumentlar va ba'zi bir bog'liq yig'indilarda birinchi umumlashtirilgan Stielts konstantasini yopiq shaklda baholash teoremasi". Raqamlar nazariyasi jurnali. 148: 537–592. arXiv:1401.3724. doi:10.1016 / j.jnt.2014.08.009.

[Alexejewsky-19] Alekseyjevskiy, V. P. (1894). "Über eine Classe von Funktionen, die der Gammafunktion analog sind" [Gamma funktsiyasiga o'xshash funktsiyalar klassi haqida]. Leypsig Vaydmanncshe Buxhandluns. 46: 268–275.

[Barnes-20] Barns, E. W. (1899). "Nazariyasi G-funktsiya ". Kvart. J. Matematik. 31: 264–314.

[Adamchik-21] Adamchik, Viktor S. (1998). "Salbiy tartibdagi poligamma funktsiyalari". J. Komput. Qo'llash. Matematika. 100 (2): 191–199. doi:10.1016 / S0377-0427 (98) 00192-7.

[Gosper-22] Gosper, R. V. (1997). " ${displaystyle extstyle int _ {n / 4} ^ {m / 6} log F (z), dz}$ maxsus funktsiyalarda, q-seriyalar va tegishli mavzular ". J. Am. Matematika. Soc. 14.

[EspinosaMoll-23] Espinosa, Olivye; Moll, Viktor H. (2002). "Xurvits Zeta funktsiyasining ba'zi integrallari to'g'risida: 1-qism". Ramanujan jurnali. 6: 159–188. doi:10.1023 / A: 1015706300169.

[Bailey-24] Beyli, Devid X.; Borwein, David; Borwein, Jonathan M. (2015). "Eulerian log-gamma integrallari va Tornxaym-Vitten zeta funktsiyalari to'g'risida". Ramanujan jurnali. 36: 43–68. doi:10.1007 / s11139-012-9427-1.

[ACEKNM-25] Amdeberhan, T .; Kofi, Mark V.; Espinosa, Olivye; Koutschan, Kristof; Manna, Dante V.; Moll, Viktor H. (2011). "Loggamma kuchlarining integrallari". Proc. Amer. Matematika. Soc. 139 (2): 535–545. doi:10.1090 / S0002-9939-2010-10589-0.

[26] E.A. Karatsuba, Transandantal funktsiyalarni tezkor baholash. Probl. Inf. Transm. 27-jild, №4, 339–360-betlar (1991).

[27] E.A. Karatsuba, Transandantal funktsiyalarni tezkor baholashning yangi usuli to'g'risida. Russ. Matematika. Surv. 46-jild, № 2, 246–247 betlar (1991).

[28] E.A. Karatsuba "Tez algoritmlar va FEE usuli ".

[29] Michon, G. P. "Trigonometriya va asosiy funktsiyalar Arxivlandi 2010 yil 9-yanvar kuni Orqaga qaytish mashinasi ". Numerika. 2007 yil 5-mayda olingan.

[30] Chaudri, M. A. va Zubair, S. M. (2001). Ilovalar bilan to'liq bo'lmagan gamma funktsiyalari klassi to'g'risida. p. 37

[31] Rays, J. A. (1995). Matematik statistika va ma'lumotlarni tahlil qilish (Ikkinchi nashr). p. 52-53

[32] Borwein, J .; Beyli, D. H. va Girgensohn, R. (2003). Matematika bo'yicha tajriba. A. K. Peters. p. 133. ISBN 978-1-56881-136-9.

[33] Eylerning qog'ozi nashr etilgan Commentarii academiae Scientificiarum Petropolitanae 5, 1738, 36-57. Qarang E19 - algebrais dari nequeunt ning transcendentibus seu kvartum termini generallari, asl maqolaning skanerlangan nusxasini o'z ichiga olgan Eyler arxividan.

[Remmert-34] Remmert, R. (2006). Murakkab funktsiyalar nazariyasidagi klassik mavzular. Kay, L. D. Springer tomonidan tarjima qilingan. ISBN 978-0-387-98221-2.

[35] Lanczos, C. (1964). "Gamma funktsiyasining aniq yaqinlashuvi". J. SIAM Numer. Anal. Ser. B. 1.

[Knuth-36] Knut, D. E. (1997). Kompyuter dasturlash san'ati, 1-jild (Asosiy algoritmlar). Addison-Uesli.

[37] Borwein, Jonathan M.; Corless, Robert M. (2017). "Oylik gamma va faktorial". Amerika matematik oyligi. Amerika matematik assotsiatsiyasi. 125 (5): 400–24. arXiv:1703.05349. Bibcode:2017arXiv170305349B. doi:10.1080/00029890.2018.1420983.

[38] Berri, M. (2001 yil aprel). "Nima uchun maxsus funktsiyalar maxsus?". Bugungi kunda fizika.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]