Kvadrat tenglama - Quadratic equation

The kvadratik formula umumiy kvadratik tenglamaning ildizlari uchun

Yilda algebra, a kvadrat tenglama (dan Lotin kvadrat uchun "kvadrat ") har qanday tenglama bo'lib, uni standart shaklda qayta tuzish mumkin

${displaystyle ax ^ {2} + bx + c = 0}$

qayerda x ifodalaydi noma'lum va a, bva v ma'lum raqamlarni ifodalaydi, qaerda a ≠ 0. Agar a = 0, keyin tenglama chiziqli, yo'q, chunki kvadratik emas ${displaystyle ax ^ {2}}$ muddat. Raqamlar a, bva v ular koeffitsientlar tenglamani va ularni mos ravishda ularni chaqirish bilan ajratish mumkin kvadratik koeffitsient, chiziqli koeffitsient va doimiy yoki bepul muddat.^[1]

Ning qiymatlari x tenglamani qanoatlantiradigan deyiladi echimlar tenglamaning va ildizlar yoki nollar ning ifoda chap tomonida. Kvadrat tenglama ko'pi bilan ikkita echimga ega. Agar yo'q bo'lsa haqiqiy echim, ikkitasi bor murakkab echimlar. Agar bitta echim bo'lsa, uni a deb aytadi er-xotin ildiz. Kvadrat tenglama har doim ikkita ildizga ega bo'ladi, agar murakkab ildizlar kiritilsa va er-xotin ildiz ikkiga hisoblansa. Kvadrat tenglama bo'lishi mumkin hisobga olingan ekvivalent tenglamaga

${displaystyle ax ^ {2} + bx + c = a (x-r) (x-s) = 0}$

qayerda r va s uchun echimlar x. Kvadrat tugatilmoqda kvadrat shakldagi tenglamada standart shakldagi natijalar kvadratik formula, jihatidan echimlarni ifodalaydi a, bva v. Kvadrat tenglamalar bilan ifodalanishi mumkin bo'lgan masalalarni echimi miloddan avvalgi 2000 yilda ma'lum bo'lgan.

Kvadrat tenglama faqat bitta noma'lumni o'z ichiga olganligi sababli, u "bir o'zgaruvchan ". Kvadrat tenglama faqat o'z ichiga oladi kuchlar ning x manfiy bo'lmagan tamsayılar va shuning uchun u a polinom tenglamasi. Xususan, bu ikkinchi daraja polinom tenglamasi, chunki eng katta kuch ikkitadir.

Kvadrat tenglamani echish

Shakl 1. Kvadratik funktsiya uchastkalari y = bolta² + bx + v, har bir koeffitsientni alohida-alohida o'zgartirish, qolgan koeffitsientlar esa (qiymatlarda) a = 1, b = 0, v = 0)

Bilan kvadratik tenglama haqiqiy yoki murakkab koeffitsientlar deb nomlangan ikkita echimga ega ildizlar. Ushbu ikkita echim bir-biridan farq qilishi yoki bo'lmasligi mumkin va ular haqiqiy bo'lishi mumkin yoki bo'lmasligi mumkin.

Tekshiruv orqali faktoring

Kvadrat tenglamani ifodalash mumkin bo'lishi mumkin bolta² + bx + v = 0 mahsulot sifatida (px + q)(rx + s) = 0. Ba'zi hollarda, oddiy tekshirish orqali, qiymatlarini aniqlash mumkin p, q, r, va s bu ikkala shaklni bir-biriga tenglashtiradigan. Agar kvadrat tenglama ikkinchi shaklda yozilgan bo'lsa, unda "Nolinchi omil xususiyati" da, agar kvadrat tenglama bajarilsa, px + q = 0 yoki rx + s = 0. Ushbu ikkita chiziqli tenglamani echish kvadratikning ildizlarini beradi.

Aksariyat talabalar uchun faktoringni tekshirish usuli ularga duch keladigan kvadratik tenglamalarni echishning birinchi usuli hisoblanadi.^{[2]:202–207} Agar biriga kvadrat tenglama berilgan bo'lsa x² + bx + v = 0, izlanayotgan faktorizatsiya shakliga ega (x + q)(x + s), va bitta ikkita raqamni topish kerak q va s qo'shadigan narsa b va kimning mahsuloti v (buni ba'zan "Vetnam qoidasi" deb ham atashadi)^[3] va bilan bog'liq Vetnam formulalari ). Misol tariqasida, x² + 5x + 6 kabi omillar (x + 3)(x + 2). Bu erda ko'proq umumiy holat a teng emas 1 tekshirish paytida aniqlanishi mumkin deb hisoblagan holda, sinov va xatolarni taxmin qilish va tekshirishda katta kuch sarflashni talab qilishi mumkin.

Qaerda kabi maxsus holatlar bundan mustasno b = 0 yoki v = 0, tekshirish bilan faktoring faqat ratsional ildizlarga ega bo'lgan kvadrat tenglamalar uchun ishlaydi. Bu shuni anglatadiki, amaliy qo'llanmalarda yuzaga keladigan kvadratik tenglamalarning aksariyatini tekshirish yordamida faktoring qilish yo'li bilan echib bo'lmaydi.^[2]:207

Kvadrat tugatilmoqda

Shakl 2. Uchun kvadratik funktsiya y = x² − x − 2, grafigi kesib o'tadigan nuqtalar x-aksis, x = −1 va x = 2, kvadrat tenglamaning echimlari x² − x − 2 = 0.

Kvadratni to'ldirish jarayonida algebraik identifikatsiyadan foydalaniladi

${displaystyle x ^ {2} + 2hx + h ^ {2} = (x + h) ^ {2},}$

bu aniq belgilangan narsani anglatadi algoritm har qanday kvadrat tenglamani echish uchun ishlatilishi mumkin.^[2]:207 Standart shakldagi kvadratik tenglamadan boshlab, bolta² + bx + v = 0

1. Ikkala tomonni ikkiga bo'ling a, kvadrat muddatning koeffitsienti.
2. Doimiy muddatni olib tashlang v/a ikkala tomondan.
3. Yarimning kvadratini qo'shing b/a, ning koeffitsienti x, ikkala tomonga. Bu "kvadratni to'ldiradi", chap tomonni mukammal kvadratga aylantiradi.
4. Chap tomonni kvadrat shaklida yozing va agar kerak bo'lsa, o'ng tomonni soddalashtiring.
5. Chap tomonning kvadrat ildizini o'ng tomonning musbat va manfiy kvadrat ildizlariga tenglashtirib ikkita chiziqli tenglamani hosil qiling.
6. Ikkala chiziqli tenglamaning har birini eching.

Ushbu algoritmdan foydalanishni biz echim bilan tasvirlaymiz 2x² + 4x − 4 = 0

${displaystyle 1) x ^ {2} + 2x-2 = 0}$

${displaystyle 2) x ^ {2} + 2x = 2}$

${displaystyle 3) x ^ {2} + 2x + 1 = 2 + 1}$

${displaystyle 4) left (x + 1ight) ^ {2} = 3}$

${displaystyle 5) x + 1 = pm {sqrt {3}}}$

${displaystyle 6) x = -1pm {sqrt {3}}}$

The plyus-minus belgisi "±" ikkalasi ham shuni ko'rsatmoqda x = −1 + √3 va x = −1 − √3 kvadrat tenglamaning echimlari.^[4]

Kvadratik formulasi va uni chiqarish

Kvadrat tugatilmoqda uchun ishlatilishi mumkin umumiy formulani chiqaring kvadrat formulasi deb nomlangan kvadratik tenglamalarni echish uchun.^[5] The matematik isbot endi qisqacha qisqacha bayon qilinadi.^[6] Buni osongina ko'rish mumkin polinom kengayishi, quyidagi tenglama kvadrat tenglamaga teng:

${displaystyle chap (x + {frac {b} {2a}} ight) ^ {2} = {frac {b ^ {2} -4ac} {4a ^ {2}}}.}$

Olish kvadrat ildiz ikkala tomonning va izolyatsiya qiluvchi xberadi:

${displaystyle x = {frac {-bpm {sqrt {b ^ {2} -4ac}}} {2a}}.}$

Ba'zi manbalar, xususan, eski manbalar kabi kvadrat tenglamaning alternativ parametrlarini qo'llaydi bolta² + 2bx + v = 0 yoki bolta² − 2bx + v = 0 ,^[7] qayerda b ehtimolligi qarama-qarshi belgi bilan, odatdagidan yarmining kattaligiga ega. Buning natijasida yechim uchun biroz boshqacha shakllar paydo bo'ladi, ammo boshqacha ekvivalentdir.

Bir qator muqobil hosilalar adabiyotda topish mumkin. Ushbu dalillar kvadrat usulini to'ldirgan standartdan soddadir, algebra bo'yicha boshqa tez-tez ishlatiladigan texnikaning qiziqarli dasturlarini aks ettiradi yoki matematikaning boshqa sohalari haqida tushuncha beradi.

Unda ma'lum bo'lgan kamroq ma'lum bo'lgan kvadratik formulalar Myuller usuli tenglama orqali bir xil ildizlarni beradi

${displaystyle x = {frac {2c} {- bpm {sqrt {b ^ {2} -4ac}}}}.}$

Buni standart kvadratik formuladan quyidagicha chiqarish mumkin Vetnam formulalari, bu ildizlarning hosilasi ekanligini tasdiqlaydi v/a.

Ushbu shaklning bitta xususiyati shundaki, u qachonki bitta to'g'ri ildiz hosil qiladi a = 0, boshqa ildiz nolga bo'linishni o'z ichiga oladi, chunki qachon a = 0, kvadrat tenglama bitta ildizga ega bo'lgan chiziqli tenglamaga aylanadi. Aksincha, bu holda, keng tarqalgan formulada bitta ildiz va an uchun nolga bo'linish mavjud noaniq shakl 0/0 boshqa ildiz uchun. Boshqa tomondan, qachon v = 0, keng tarqalgan formuladan ikkita to'g'ri ildiz olinadi, bu shakl nol ildizni va noaniq shaklni beradi 0/0.

Kvadrat tenglama kamaytirilgan

Ba'zan kvadrat tenglamani shunday qilib kamaytirish juda qulaydir etakchi koeffitsient bitta. Bu ikkala tomonni ikkiga bo'lish orqali amalga oshiriladi a, chunki bu har doim ham mumkin a nolga teng emas. Bu ishlab chiqaradi qisqartirilgan kvadrat tenglama:^[8]

${displaystyle x ^ {2} + px + q = 0,}$

qayerda p = b/a va q = v/a. Bu monik tenglama asl nusxasi bilan bir xil echimlarga ega.

Koydirilgan kvadrat tenglama echimlari uchun uning koeffitsientlari bo'yicha yozilgan kvadratik formulasi:

${displaystyle x = {frac {1} {2}} chap (-ppm {sqrt {p ^ {2} -4q}} ight),}$

yoki unga teng ravishda:

${displaystyle x = - {frac {p} {2}} pm {sqrt {left ({frac {p} {2}} ight) ^ {2} -q}}.}$

Diskriminant

Shakl 3. Diskriminant belgilar

Kvadratik formulada kvadrat ildiz belgisi ostidagi ifoda deyiladi diskriminant kvadrat tenglamaning koeffitsienti va ko'pincha katta harf yordamida ifodalanadi D. yoki katta harf yunoncha delta:^[9]

${displaystyle Delta = b ^ {2} -4ac.}$

Bilan kvadratik tenglama haqiqiy koeffitsientlar bir yoki ikkita aniq haqiqiy ildizga yoki ikkita aniq murakkab ildizga ega bo'lishi mumkin. Bu holda diskriminant ildizlarning sonini va xususiyatini belgilaydi. Uchta holat mavjud:

• Agar diskriminant ijobiy bo'lsa, unda ikkita alohida ildiz mavjud

${displaystyle {frac {-b + {sqrt {Delta}}} {2a}} quad {ext {and}} quad {frac {-b- {sqrt {Delta}}} {2a}},}$

ikkalasi ham haqiqiy sonlar. Bilan kvadratik tenglamalar uchun oqilona koeffitsientlar, agar diskriminant a kvadrat raqam, keyin ildizlar oqilona - boshqa hollarda ular bo'lishi mumkin kvadratik irratsionalliklar.

• Agar diskriminant nolga teng bo'lsa, unda aynan bittasi bor haqiqiy ildiz

${displaystyle - {frac {b} {2a}},}$

ba'zan takrorlangan yoki er-xotin ildiz.

• Agar diskriminant salbiy bo'lsa, unda haqiqiy ildizlar yo'q. Aksincha, ikkita alohida (haqiqiy bo'lmagan) mavjud murakkab ildizlar^[10]

${displaystyle - {frac {b} {2a}} + i {frac {sqrt {-Delta}} {2a}} quad {ext {and}} quad - {frac {b} {2a}} - i {frac { sqrt {-Delta}} {2a}},}$

qaysiki murakkab konjugatlar bir-birining. Ushbu iboralarda men bo'ladi xayoliy birlik.

Shunday qilib, agar diskriminant nolga teng bo'lmagan taqdirda, ildizlar aniq, agar diskriminant salbiy bo'lmagan taqdirda, ildizlar haqiqiydir.

Geometrik talqin

Grafigi y = bolta² + bx + v, qayerda a va diskriminant b² − 4ak ijobiy, bilan

• Ildizlar va y- kirish qizil
• Vertikal va simmetriya o'qi in ko'k
• Fokus va direktoriya pushti

Ning murakkab ildizlarini ingl y = bolta² + bx + v: parabola tepasiga nisbatan 180 ° burilgan (apelsin). Uning x- kesmalar o'zlarining o'rta nuqtasi atrofida 90 ° ga aylantiriladi va dekartiya tekisligi murakkab tekislik sifatida talqin etiladi (yashil).^[11]

Funktsiya f(x) = bolta² + bx + v a kvadratik funktsiya.^[12] Har qanday kvadratik funktsiyaning grafigi bir xil umumiy shaklga ega, u a deb nomlanadi parabola. Parabolaning joylashishi va kattaligi va qanday ochilishi, ning qiymatlariga bog'liq a, bva v. 1-rasmda ko'rsatilgandek, agar a > 0, parabola minimal nuqtaga ega va yuqoriga qarab ochiladi. Agar a < 0, parabola maksimal nuqtaga ega va pastga qarab ochiladi. Parabolaning haddan tashqari nuqtasi, minimal yoki maksimal bo'lsin, unga to'g'ri keladi tepalik. The x- muvofiqlashtirish tepalik joylashgan bo'ladi ${displaystyle scriptstyle x = {frac {-b} {2a}}}$, va y- muvofiqlashtirish tepaga buni almashtirish orqali topish mumkin x- qiymat funktsiyaga. The y- to'siq nuqtada joylashgan (0, v).

Kvadrat tenglamaning echimlari bolta² + bx + v = 0 ga mos keladi ildizlar funktsiyasi f(x) = bolta² + bx + v, chunki ular qiymatlari x buning uchun f(x) = 0. 2-rasmda ko'rsatilgandek, agar a, bva v bor haqiqiy raqamlar va domen ning f haqiqiy sonlar to'plami, keyin ildizlari f aynan shunday x-koordinatalar ga tegib turgan nuqtalarning x-aksis. 3-rasmda ko'rsatilgandek, agar diskriminant ijobiy bo'lsa, grafik unga tegadi x-aksis ikki nuqtada; agar nol bo'lsa, grafik bir nuqtaga tegadi; agar manfiy bo'lsa, grafik ga tegmaydi x-aksis.

Kvadrat faktorizatsiya

Atama

${displaystyle x-r}$

polinomning koeffitsienti hisoblanadi

${displaystyle ax ^ {2} + bx + c}$

agar va faqat agar r a ildiz kvadrat tenglamaning

${displaystyle ax ^ {2} + bx + c = 0.}$

Bu kvadratik formuladan kelib chiqadi

${displaystyle ax ^ {2} + bx + c = aleft (x- {frac {-b + {sqrt {b ^ {2} -4ac}}} {2a}} ight) chap (x- {frac {-b-) {sqrt {b ^ {2} -4ac}}} {2a}} kech).}$

Maxsus holatda b² = 4ak bu erda kvadratik faqat bitta aniq ildizga ega (ya'ni diskriminant nolga teng), kvadratik polinom bo'lishi mumkin hisobga olingan kabi

${displaystyle ax ^ {2} + bx + c = aleft (x + {frac {b} {2a}} ight) ^ {2}.}$

Grafik echim

Shakl 4. Kvadrat tenglamaning ikkita ildizidan birini grafik hisoblash kalkulyatori bilan hisoblash 2x² + 4x − 4 = 0. Displeyda faqat beshta muhim aniqlik ko'rsatilgan bo'lsa-da, olingan qiymat xc 0,732050807569 ga teng, o'n ikki muhim ko'rsatkichga to'g'ri keladi.

Haqiqiy ildizsiz kvadratik funktsiya: y = (x − 5)² + 9. "3" - bu hayoliy qism x- to'siq. Haqiqiy qism x- tepalik koordinatasi. Shunday qilib, ildizlar 5 ± 3men.

Kvadrat tenglamaning echimlari

${displaystyle ax ^ {2} + bx + c = 0}$

dan chiqarilishi mumkin grafik ning kvadratik funktsiya

${displaystyle y = ax ^ {2} + bx + c,}$

bu parabola.

Agar parabola x- ikkita nuqtada eksa, ikkita haqiqiy mavjud ildizlar, qaysi x-bu ikki nuqtaning koordinatalari (shuningdek, shunday deyiladi) x-tushunish).

Agar parabola bo'lsa teginish uchun x-aksis, er-xotin ildiz bor, u x-graf va parabola orasidagi aloqa nuqtasining koordinatasi.

Agar parabola bilan kesishmasa x-aksis, ikkitasi bor murakkab konjugat ildizlar. Garchi bu ildizlarni grafikada tasavvur qilish mumkin bo'lmasa ham, ularning haqiqiy va xayoliy qismlar bolishi mumkin.^[13]

Ruxsat bering h va k tegishli ravishda x-koordinat va y- parabola tepasining koordinatasi (bu maksimal yoki minimal bo'lgan nuqta y- muvofiqlashtirish. Kvadratik funktsiya qayta yozilishi mumkin

${displaystyle y = a (x-h) ^ {2} + k.}$

Ruxsat bering d ning nuqtasi orasidagi masofa bo'lsin y- muvofiqlashtirish 2k parabola o'qida va xuddi shu bilan parabola ustidagi nuqta y-koordinat (rasmga qarang; parabola simmetriyasi tufayli bir xil masofani beradigan ikkita nuqta bor). Keyin ildizlarning haqiqiy qismi hva ularning xayoliy qismi ±d. Ya'ni, ildizlar

${displaystyle h + idquad {ext {and}} quad x-id,}$

yoki rasmning misolida

${displaystyle 5 + 3iquad {ext {and}} quad 5-3i.}$

Ahamiyatni yo'qotishdan saqlanish

Kvadratik formula aniq echimni taqdim etgan bo'lsa-da, natija aniq emas haqiqiy raqamlar hisoblash paytida odatdagidek taxmin qilinadi raqamli tahlil, bu erda haqiqiy sonlar taxminan bilan taqqoslanadi suzuvchi nuqta raqamlari (ko'pchilikda "real" deb nomlanadi dasturlash tillari ). Shu nuqtai nazardan kvadratik formula to'liq emas barqaror.

Bu ildizlar har xil bo'lganda paydo bo'ladi kattalik tartibi, yoki ekvivalent ravishda, qachon b² va b² − 4ak kattaligi bo'yicha yaqin. Bunday holda, deyarli teng bo'lgan ikkita raqamni olib tashlash sabab bo'ladi ahamiyatini yo'qotish yoki halokatli bekor qilish kichikroq ildizda. Bunga yo'l qo'ymaslik uchun kattaligi kichikroq bo'lgan ildiz, r, sifatida hisoblash mumkin ${displaystyle (c / a) / R}$ qayerda R kattaligi kattaroq bo'lgan ildiz.

Shartlar orasida bekor qilishning ikkinchi shakli bo'lishi mumkin b² va 4ak diskriminantning, ya'ni ikkala ildiz juda yaqin bo'lganda. Bu ildizlardagi to'g'ri raqamlarning yarmigacha yo'qolishiga olib kelishi mumkin.^[7][14]

Misollar va ilovalar

Jarlik sakrashchining traektoriyasi parabolik chunki gorizontal siljish vaqtning chiziqli funksiyasi ${displaystyle x = v_ {x} t}$, vertikal siljish esa vaqtning kvadratik funktsiyasi ${displaystyle y = {frac {1} {2}} da ^ {2} + v_ {y} t + h}$. Natijada, yo'l kvadrat tenglamaga amal qiladi ${displaystyle y = {frac {a} {2v_ {x} ^ {2}}} x ^ {2} + {frac {v_ {y}} {v_ {x}}} x + h}$, qayerda ${displaystyle v_ {x}}$ va ${displaystyle v_ {y}}$ dastlabki tezlikning gorizontal va vertikal komponentlari, a bu tortishish kuchi tezlashtirish va h asl balandlik. The a bu erda qiymat salbiy deb hisoblanishi kerak, chunki uning yo'nalishi (pastga) balandlik o'lchoviga qarama-qarshi (yuqoriga).

The oltin nisbat kvadrat tenglamaning ijobiy yechimi sifatida topiladi ${displaystyle x ^ {2} -x-1 = 0.}$

Ning tenglamalari doira va boshqasi konusning qismlari —ellipslar, parabolalar va giperbolalar - ikkita o'zgaruvchidagi kvadrat tenglamalar.

hisobga olib kosinus yoki sinus kosinusi yoki sinusini topuvchi burchakning yarim baravar katta bo'lgan burchak kvadrat tenglamani echishni o'z ichiga oladi.

Bilan bog'liq iboralarni soddalashtirish jarayoni boshqa bir ifodaning kvadrat ildizini o'z ichiga olgan ifodaning kvadrat ildizi kvadrat tenglamaning ikkita echimini topishni o'z ichiga oladi.

Dekart teoremasi har to'rt o'pish (o'zaro ta'sirli) doiralar uchun ularning radiusi ma'lum bir kvadrat tenglamani qondirish.

Tomonidan berilgan tenglama Fuss teoremasi, a radiusi orasidagi munosabatni berish bisentrik to'rtburchak "s yozilgan doira, uning radiusi cheklangan doira va shu doiralar markazlari orasidagi masofani kvadrat tenglama sifatida ifodalash mumkin, buning uchun ikkala doiraning markazlari orasidagi masofa ularning radiusi bo'yicha echimlardan biri hisoblanadi. Tegishli radius bo'yicha bir xil tenglamaning boshqa echimi aylana doirasi markazi bilan markazining orasidagi masofani beradi atrofi ning sobiq tangensial to'rtburchak.

Tarix

Bobil matematiklari, miloddan avvalgi 2000 yildayoq (ko'rsatilgan Qadimgi Bobil gil tabletkalar ) to'rtburchaklar maydonlari va tomonlari bilan bog'liq muammolarni hal qilishi mumkin. Ushbu algoritmga qadar bo'lgan dalillar mavjud Urning uchinchi sulolasi.^[15] Zamonaviy notatsiyada, odatda, bir vaqtning o'zida shaklning bir vaqtning o'zida tenglamalarini echish bilan bog'liq muammolar:

${displaystyle x + y = p, xy = q,}$

bu so'z bilan tengdir x va y tenglamaning ildizlari:^[16]:86

${displaystyle z ^ {2} + q = pz.}$

Yuqoridagi to'rtburchaklar masalasini hal qilish uchun Bobil yozuvchilari tomonidan berilgan qadamlar x va y, quyidagilar edi:

1. Yarim qismini hisoblang p.
2. Natija kvadratini.
3. Chiqaring q.
4. Kvadratchalar jadvali yordamida (musbat) kvadrat ildizni toping.
5. Berish uchun (1) va (4) bosqichlarining natijalarini qo'shib qo'ying x.

Zamonaviy yozuvlarda bu hisoblashni anglatadi ${displaystyle x = left ({frac {p} {2}} ight) + {sqrt {left ({frac {p} {2}} ight) ^ {2} -q}}}$, bu zamonaviy kunga teng kvadratik formula kattaroq haqiqiy ildiz uchun (agar mavjud bo'lsa) ${displaystyle x = {frac {-b + {sqrt {b ^ {2} -4ac}}} {2a}}}$ bilan a = 1, b = −pva v = q.

Bobil, Misr, Gretsiya, Xitoy va Hindistonda kvadrat tenglamalarni echishda geometrik usullardan foydalanilgan. Misrlik Berlin papirusi, orqaga qaytish O'rta qirollik (Miloddan avvalgi 2050 yildan milodgacha 1650 yilgacha), ikki davrli kvadrat tenglamaning echimini o'z ichiga oladi.^[17] Miloddan avvalgi 400-yillarda Bobil matematiklari va Xitoy matematiklari miloddan avvalgi 200 yilgacha ishlatilgan dissektsiyaning geometrik usullari ijobiy ildizlarga ega kvadrat tenglamalarni echish.^[18][19] Kvadrat tenglamalar uchun qoidalar berilgan Matematik san'atning to'qqiz boblari, matematikaga oid Xitoy risolasi.^[19][20] Ushbu dastlabki geometrik usullar umumiy formulaga ega bo'lmaganga o'xshaydi. Evklid, Yunonistonlik matematik, miloddan avvalgi 300 yillarda yanada mavhum geometrik usul ishlab chiqardi. Faqatgina geometrik yondashuv bilan Pifagoralar va Evklid kvadrat tenglama echimlarini topishning umumiy protsedurasini yaratdi. Uning ishida Arifmetika, yunon matematikasi Diofant kvadrat tenglamani echdi, lekin ikkala ildiz ham musbat bo'lgan taqdirda ham, faqat bitta ildiz beradi.^[21]

Milodiy 628 yilda, Braxmagupta, an Hind matematikasi, kvadrat tenglamaning birinchi aniq echimini (hanuzgacha to'liq umumiy bo'lmagan) berdi bolta² + bx = v quyidagicha: "[kvadrat koeffitsienti] ning to'rt baravariga ko'paytirilgan absolyut songa [o'rta koeffitsient] kvadratini qo'shing; bir xil kvadrat ildizga, [o'rta koeffitsientiga] kamroq, kvadratning [koeffitsienti] ning ikki baravariga bo'linishi bu qiymatdir. " (Brahmasphutasiddhanta, Colebrook tarjimasi, 1817, 346 bet)^[16]:87 Bu quyidagilarga teng:

${displaystyle x = {frac {{sqrt {4ac + b ^ {2}}} - b} {2a}}.}$

The Baxshali qo'lyozmasi milodiy VII asrda Hindistonda yozilgan, kvadrat tenglamalarni echishning algebraik formulasi bilan bir qatorda kvadratik noaniq tenglamalar (dastlab turi bolta/v = y^{[tushuntirish kerak : bu kvadratik emas, chiziqli]}). Muhammad ibn Muso al-Xorazmiy (Fors, 9-asr), Brahmagupta tomonidan ilhomlangan,^{[asl tadqiqotmi? ]} ijobiy echimlar uchun ishlaydigan formulalar to'plamini ishlab chiqdi. Al-Xorazmiy umumiy kvadratik tenglamani to'liq echimini taqdim etishda davom etadi, har kvadratik tenglama uchun bitta yoki ikkita raqamli javobni qabul qiladi, shu bilan birga geometrik dalillar jarayonida.^[22] Shuningdek, u kvadratni to'ldirish usulini tasvirlab berdi va buni tan oldi diskriminant ijobiy bo'lishi kerak,^[22][23]:230 bu uning zamondoshi tomonidan isbotlangan Abd al-Hamud ibn Turk (O'rta Osiyo, 9-asr), agar diskriminant manfiy bo'lsa, kvadrat tenglamada echim yo'qligini isbotlash uchun geometrik raqamlar bergan.^[23]:234 Al-Xorazmiyning o'zi salbiy echimlarni qabul qilmagan bo'lsa-da, keyinchalik Islom matematiklari uning o'rniga kelgan salbiy echimlarni qabul qildi,^[22]:191 shu qatorda; shu bilan birga mantiqsiz raqamlar echimlar sifatida.^[24] Abu Komil Shuja ibn Aslam (Misr, X asr), xususan, birinchi bo'lib irratsional sonlarni qabul qildi (ko'pincha a shaklida) kvadrat ildiz, kub ildizi yoki to'rtinchi ildiz ) kvadrat tenglamalarga echimlar sifatida yoki koeffitsientlar tenglamada.^[25] 9-asr hind matematikasi Sridxara kvadrat tenglamalarni echish qoidalarini yozdi.^[26]

Yahudiy matematik Ibrohim bar Xiyya Xa-Nasi (12-asr, Ispaniya) umumiy kvadratik tenglamaning to'liq echimini o'z ichiga olgan birinchi Evropa kitobining muallifi.^[27] Uning echimi asosan Al-Xorazmiyning asarlariga asoslangan edi.^[22] Xitoy matematikasining yozuvi Yang Xui (Milodiy 1238–1298) - bu "x" ning salbiy koeffitsientlari bo'lgan kvadrat tenglamalar paydo bo'lgan birinchi ma'lum, ammo u buni avvalgi holatga bog'laydi Lyu Yi.^[28] 1545 yilga kelib Gerolamo Kardano kvadrat tenglamalar bilan bog'liq ishlarni tuzdi. Barcha holatlarni o'z ichiga olgan kvadratik formulani birinchi tomonidan olingan Simon Stevin 1594 yilda.^[29] 1637 yilda Rene Dekart nashr etilgan La Géémetrie bugungi kunda biz bilgan shaklda kvadratik formulani o'z ichiga olgan.

Murakkab mavzular

Ildizni hisoblashning alternativ usullari

Vetnam formulalari

Shakl 5. Vetnamning kvadrat tenglamaning ikkita ildizidan kichikrog'i uchun yaqinlashishi orasidagi farqning grafigi x² + bx + v = 0 kvadratik formuladan foydalanib hisoblangan qiymat bilan solishtirganda. Vetanning taxminiy qiymati kichik uchun noto'g'ri b lekin katta uchun aniq b. Kvadratik formuladan foydalangan holda to'g'ridan-to'g'ri baholash kichik uchun aniqdir b taqqoslanadigan qiymatga ega, ammo katta ahamiyatga ega bo'lgan xatolarni yo'qotadi b va keng tarqalgan ildizlar. Vietnamning yaqinlashishi o'rtasidagi farq ga qarshi to'g'ridan-to'g'ri hisoblash katta nuqtalarda minimal darajaga etadi va yaxlitlash bu minimal darajadan yuqori egri chiziqlarda chayqalishni keltirib chiqaradi.

Vetnam formulalari ko'pburchakning ildizlari va uning koeffitsientlari o'rtasida oddiy munosabatlarni beradi. Kvadratik polinom uchun ular quyidagi shaklga ega:

${displaystyle x_ {1} + x_ {2} = - {frac {b} {a}}}$

va

${displaystyle x_ {1} x_ {2} = {frac {c} {a}}.}$

Ushbu natijalar aloqadan darhol kelib chiqadi:

${displaystyle left (x-x_ {1} ight) left (x-x_ {2} ight) = x ^ {2} -left (x_ {1} + x_ {2} ight) x + x_ {1} x_ { 2} = 0,}$

bu muddat bilan atama bilan taqqoslanishi mumkin

${displaystyle x ^ {2} + (b / a) x + c / a = 0.}$

Yuqoridagi birinchi formuladan kvadratik funktsiyani grafikalashda qulay ifoda olinadi. Grafik vertikal chiziqqa nisbatan nosimmetrik bo'lgani uchun tepalik, ikkita haqiqiy ildiz mavjud bo'lganda, vertex x-koordinat ildizlarning (yoki kesmalarning) o'rtacha qismida joylashgan. Shunday qilib x-tepaning koordinatasi ifoda bilan berilgan

${displaystyle x_ {V} = {frac {x_ {1} + x_ {2}} {2}} = - {frac {b} {2a}}.}$

The y-koordinatani yuqoridagi natijani berilgan kvadrat tenglamaga almashtirish orqali olish orqali olish mumkin

${displaystyle y_ {V} = - {frac {b ^ {2}} {4a}} + c = - {frac {b ^ {2} -4ac} {4a}}.}$

Amaliy masala sifatida Vetnam formulalari kvadratning ildizlarini topish uchun foydali usulni beradi, agar bitta ildiz boshqasidan ancha kichik bo'lsa. Agar | x ₂| << | x ₁|, keyin x ₁ + x ₂ ≈ x ₁va bizda shunday taxmin bor:

${displaystyle x_ {1} taxminan - {frac {b} {a}}.}$

Vetnamning ikkinchi formulasida quyidagilar mavjud:

${displaystyle x_ {2} = {frac {c} {ax_ {1}}} taxminan - {frac {c} {b}}.}$

Ushbu formulalarni kvadratik formuladan bitta katta va bitta kichik ildiz sharti bilan baholash ancha oson, chunki kvadratik formula kichik ildizni deyarli teng bo'lgan ikkita sonning farqi (katta b), bu sabab bo'ladi yumaloq xato raqamli baholashda. 5-rasmda kvadratik formuladan foydalangan holda (i) to'g'ridan-to'g'ri baholash (ildizlar qiymat jihatidan bir-biriga yaqin bo'lganida aniq) va (ii) Vetnam formulalarining yuqoridagi yaqinlashishiga asoslangan baho (ildizlar keng joylashganda aniq) o'rtasidagi farq ko'rsatilgan. ). Lineer koeffitsient sifatida b ortadi, dastlab kvadratik formulasi aniq va taxminiy formulasi aniqlikda yaxshilanadi, bu usullar orasidagi kichik farqga olib keladi b ortadi. Biroq, biron bir vaqtda kvadrat formulasi yumaloq xato tufayli aniqlikni yo'qotishni boshlaydi, taxminiy usul esa yaxshilanishda davom etadi. Binobarin, kvadrat formulasi tobora yomonlashib borishi bilan usullar orasidagi farq ortib boraveradi.

Bunday holat odatda kuchaytirgich dizaynida paydo bo'ladi, bu erda barqaror ishlashni ta'minlash uchun keng ajratilgan ildizlar talab qilinadi (qarang) qadam javob ).

Trigonometrik eritma

Kalkulyatorlardan bir necha kun oldin odamlar foydalanishadi matematik jadvallar - hisoblash natijalarini har xil argumentlar bilan ko'rsatadigan raqamlar ro'yxati - hisoblashni soddalashtirish va tezlashtirish uchun. Matematika va tabiiy darsliklarda logarifmalar va trigonometrik funktsiyalar jadvallari keng tarqalgan edi. Astronomiya, samoviy navigatsiya va statistika kabi ilovalar uchun ixtisoslashgan jadvallar nashr etildi. Raqamli yaqinlashtirish usullari mavjud edi, deyiladi prostaferez, bu ko'paytirish va kuch va ildizlarni olish kabi ko'p vaqt sarflaydigan operatsiyalar atrofida yorliqlarni taklif qildi.^[30] Astronomlar, ayniqsa, hisob-kitoblarning uzoq qatorini tezlashtirishi mumkin bo'lgan usullardan xavotirda edilar samoviy mexanika hisob-kitoblar.

Aynan shu nuqtai nazardan biz kvadrat tenglamalarni trigonometrik almashtirish yordamida echish vositalarining rivojlanishini tushunamiz. Kvadrat tenglamaning quyidagi muqobil shaklini ko'rib chiqing,

[1]   ${displaystyle ax ^ {2} + bxpm c = 0,}$

bu erda ± belgisining belgisi shunday tanlangan a va v ikkalasi ham ijobiy bo'lishi mumkin. O'zgartirish bilan

[2]   ${displaystyle x = {sqrt {c / a}} heta}$

va keyin orqali ko'paytiriladi cos²θ, biz olamiz

[3]   ${displaystyle sin ^ {2} heta + {frac {b} {sqrt {ac}}} sin heta cos heta pm cos ^ {2} heta = 0.}$

Funktsiyalari bilan tanishtirish 2θ va qayta tashkil etish, biz olamiz

[4]   ${displaystyle an 2 heta _ {n} = + 2 {frac {sqrt {ac}} {b}},}$

[5]   ${displaystyle sin 2 heta _ {p} = - 2 {frac {sqrt {ac}} {b}},}$

obunalar qaerda n va p tenglamada manfiy yoki musbat belgidan foydalanishga mos ravishda mos keladi [1]. Ning ikkita qiymatini almashtirish θ_n yoki θ_p tenglamalardan topilgan [4] yoki [5] ichiga [2] ning zarur ildizlarini beradi [1]. Murakkab ildizlar tenglamaga asoslangan eritmada uchraydi [5] agar ning mutlaq qiymati bo'lsa gunoh 2θ_p birlikdan oshib ketadi. Ushbu aralash trigonometrik va logarifmik jadvalni qidirish strategiyasidan foydalangan holda kvadratik tenglamalarni echishda sarf qilingan sa'y-harakatlar faqat logaritmik jadvallar yordamida qilingan harakatlarning uchdan ikki qismini tashkil etdi.^[31] Murakkab ildizlarni hisoblash uchun boshqa trigonometrik shakldan foydalanish kerak bo'ladi.^[32]

Buni tasavvur qilish uchun keling, bizda yetti o'rinli logaritma va trigonometrik jadvallar mavjud bo'lib, quyidagilarni oltita muhim raqamli aniqlikda hal qilishni xohlaymiz:

${displaystyle 4.16130x ^ {2} + 9.15933x-11.4207 = 0}$

1. Etti o'rinli qidiruv jadvali faqat 100000 ta yozuvga ega bo'lishi mumkin va oraliq natijalarni etti joyga hisoblash, odatda qo'shni yozuvlar o'rtasida interpolatsiyani talab qiladi.
2. ${displaystyle log a = 0.6192290, log b = 0.9618637, log c = 1.0576927}$
3. ${displaystyle 2 {sqrt {ac}} / b = 2 imes 10 ^ {(0.6192290 + 1.0576927) /2-0.9618637} = 1.505314}$
4. ${displaystyle heta = (an ^ {- 1} 1.505314) /2=28.20169^ {circ} {ext {or}} - 61.79831 ^ {circ}}$
5. ${displaystyle log | heta | = -0.2706462 {ext {yoki}} 0.2706462}$
6. ${displaystyle log {sqrt {c / a}} = (1.0576927-0.6192290) /2=0.2192318}$
7. ${displaystyle x_ {1} = 10 ^ {0.2192318-0.2706462} = 0.888353}$ (oltita muhim raqamga yaxlitlangan)

${displaystyle x_ {2} = - 10 ^ {0.2192318 + 0.2706462} = - 3.08943}$

Polar koordinatalardagi murakkab ildizlar uchun echim

Agar kvadrat tenglama bo'lsa ${displaystyle ax ^ {2} + bx + c = 0}$ haqiqiy koeffitsientlar ikkita murakkab ildizga ega - bu holda ${displaystyle b ^ {2} -4ac <0,}$ talab qilmoqda a va v bir-birlari bilan bir xil belgiga ega bo'lish uchun - u holda ildizlar uchun echimlarni qutb shaklida ifodalash mumkin^[33]

${displaystyle x_ {1} ,, x_ {2} = r (cos heta pm isin heta),}$

qayerda ${displaystyle r = {sqrt {frac {c} {a}}}}$ va ${displaystyle heta = cos ^ {- 1} chap ({frac {-b} {2 {sqrt {ac}}}} ight).$

Geometrik eritma

Shakl 6. ning geometrik eritmasi bolta² + bx + v = 0 Lill usuli yordamida. Yechimlar −AX1 / SA, −AX2 / SA

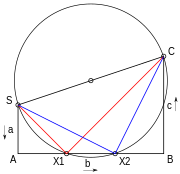
Kvadrat tenglama geometrik usulda bir necha usul bilan echilishi mumkin. Bitta usul orqali Lill usuli. Uch koeffitsient a, b, v 6-rasmda SA, AB va BC da bo'lgani kabi ular orasidagi to'g'ri burchaklar bilan chizilgan, diametri SC boshlanish va tugash nuqtasi bilan aylana chizilgan. Agar bu uchlikning AB chizig'ini kesgan bo'lsa, unda tenglama yechimga ega bo'ladi va echimlar A dan bu chiziq bo'ylab masofaning salbiy koeffitsienti bilan birinchi koeffitsientga bo'linadi. a yoki SA. Agar a bu 1 koeffitsientlar to'g'ridan-to'g'ri o'chirilishi mumkin. Shunday qilib, diagrammadagi echimlar -AX1 / SA va -AX2 / SA.^[34]

Kvadrat tenglamaning karlyel doirasi x² − sx + p = 0.

The Karlyl doirasi nomi bilan nomlangan Tomas Karleyl, kvadrat tenglamaning echimlari aylananing bilan kesmalarining gorizontal koordinatalari ekanligi xususiyatiga ega gorizontal o'q.^[35] Rivojlanish uchun karlyl doiralari ishlatilgan chiziqli va kompasli konstruksiyalar ning muntazam ko'pburchaklar.

Kvadrat tenglamani umumlashtirish

Agar koeffitsientlar bo'lsa, formula va uning chiqarilishi to'g'ri bo'lib qoladi a, b va v bor murakkab sonlar, yoki umuman olganda har qanday a'zolar maydon kimning xarakterli emas 2. (2 xarakteristikasi sohasida, element 2a nolga teng va uni ajratish mumkin emas.)

Belgisi

${displaystyle pm {sqrt {b ^ {2} -4ac}}}$

formulada "kvadrati bo'lgan ikki elementdan biri sifatida tushunilishi kerak b² − 4ak, agar bunday elementlar mavjud bo'lsa ". Ba'zi maydonlarda ba'zi elementlarning kvadrat ildizi yo'q, ba'zilarining ikkitasi bor; faqat nolga bitta kvadrat ildiz kiradi, faqat xarakterli maydonlardan tashqari 2. Maydonda biron bir sonning kvadrat ildizi bo'lmasa ham, har doim ham kvadrat mavjud kengaytma maydoni bu shunday qiladi, shuning uchun kvadratik formula doimo ushbu kengaytma maydonidagi formula sifatida mantiqiy bo'ladi.

Xarakterli 2

Xarakterli sohada 2, tayanadigan kvadratik formula 2 bo'lish a birlik, ushlab turmaydi. Ni ko'rib chiqing monik kvadratik polinom

${displaystyle x ^ {2} + bx + c}$

xarakterli maydon bo'yicha 2. Agar b = 0, keyin eritma kvadrat ildiz chiqarishga kamayadi, shuning uchun eritma bo'ladi

${displaystyle x = {sqrt {c}}}$

va shundan beri faqat bitta ildiz bor

${displaystyle - {sqrt {c}} = - {sqrt {c}} + 2 {sqrt {c}} = {sqrt {c}}.}$

Qisqa bayoni; yakunida,

${displaystyle displaystyle x ^ {2} + c = (x + {sqrt {c}}) ^ {2}.}$

Qarang kvadratik qoldiq cheklangan maydonlarda kvadrat ildizlarni ajratib olish haqida ko'proq ma'lumot olish uchun.

Bunday holda b ≠ 0, ikkita alohida ildiz bor, lekin agar polinom bo'lsa qisqartirilmaydi, ularni koeffitsient sohasidagi sonlarning kvadrat ildizlari bilan ifodalash mumkin emas. Buning o'rniga 2-ildiz R(v) ning v polinomning ildizi bo'lish x² + x + v, ning elementi bo'linish maydoni bu polinom. Buni tasdiqlaydi R(v) + 1 shuningdek, ildizdir. Ikkala ildizli operatsiya nuqtai nazaridan (monik bo'lmagan) kvadratikaning ikkita ildizi bolta² + bx + v bor

${displaystyle {frac {b} {a}} Rleft ({frac {ac} {b ^ {2}}} ight)}$

va

${displaystyle {frac {b} {a}} chap (Rleft ({frac {ac} {b ^ {2}}} ight) + 1ight).}$

Masalan, ruxsat bering a birliklari guruhining multiplikativ generatorini belgilang F₄, Galois maydoni to'rtinchi buyurtma (shunday qilib a va a + 1 ning ildizlari x² + x + 1 ustida F₄. Chunki (a + 1)² = a, a + 1 kvadrat tenglamaning noyob echimi x² + a = 0. Boshqa tomondan, polinom x² + bolta + 1 qisqartirilmaydi F₄, lekin u bo'linadi F₁₆, u erda ikkita ildiz bor ab va ab + a, qayerda b ning ildizi x² + x + a yilda F₁₆.

Bu alohida holat Artin-Shrayer nazariyasi.

Shuningdek qarang

• Doimiy kasrlar bilan kvadratik tenglamalarni echish
• Lineer tenglama
• Kubik funktsiyasi
• Kvartatik tenglama
• Kvintik tenglama
• Algebraning asosiy teoremasi

Adabiyotlar

Tashqi havolalar

• "Kvadrat tenglama", Matematika entsiklopediyasi, EMS Press, 2001 [1994]
• Vayshteyn, Erik V. "Kvadrat tenglamalar". MathWorld.
• Kvadrat tenglamadan 101 ta foydalanish
• Kvadrat tenglamadan 101 ta foydalanish: II qism