Cramers paradoks - Cramers paradox - Wikipedia
Yilda matematika, Kramer paradoksi yoki Kramer-Eyler paradoksi[1] ning ikkita yuqori tartibli egri chiziqning kesishish nuqtalari soni samolyot odatda shunday egri chiziqlardan birini aniqlash uchun zarur bo'lgan ixtiyoriy nuqtalar sonidan kattaroq bo'lishi mumkin. Uning nomi bilan nomlangan Jenevan matematik Gabriel Kramer.
Ushbu paradoks ikki teoremani sodda tushunish yoki noto'g'ri qo'llash natijasidir:
- Bezut teoremasi (ikkitasining kesishish nuqtalari soni algebraik egri chiziqlar ma'lum darajadagi shartlar bajarilishi sharti bilan ularning darajalari ko'paytmasiga teng).
- Kramer teoremasi (daraja egri n tomonidan belgilanadi n(n + 3) / 2 ball, yana ba'zi shartlar mavjud deb hisoblasak).
Buni hamma uchun kuzatib boring n ≥ 3, n2 ≥ n(n + 3) / 2, shuning uchun uch yoki undan yuqori darajalar uchun ikkala egri chiziqlar bilan o'rtoqlashadigan etarli miqdordagi nuqta bo'lishi mumkin edi, chunki bu nuqtalar egri chiziqlardan birini aniq belgilashi kerak.
Paradoksning echimi shundaki, ba'zi degenerativ holatlarda n(n + 3) / 2 ball egri chiziqni noyob tarzda aniqlash uchun etarli emas.
Tarix
Paradoks birinchi marta tomonidan nashr etilgan Kolin Maklaurin.[2][3] Kramer va Leonhard Eyler paradoks bo'yicha 1744 va 1745 yilgi xatlar bilan mos tushdi va Eyler Kramerga muammoni tushuntirdi.[4] Sifatida tanilgan Kramer paradoksi uning 1750 kitobida ko'rsatilganidan keyin Kirish à l'analyse des lignes courbes algébriques, garchi Kramer bayonotning manbai sifatida Maklaurinni keltirgan.[5] Taxminan bir vaqtning o'zida Eyler 9 ball bilan yagona aniqlanmagan kubik egri chizig'ini ko'rsatadigan misollarni nashr etdi[4][6] va muammoni o'z kitobida muhokama qildi Analysis infinitorum-ga kirish. Natijada e'lon qilindi Jeyms Stirling va tomonidan izohlangan Yulius Pluker.[1]
Chiziqlar va noaniq konuslar uchun paradoks yo'q
Birinchi tartib egri chiziqlari uchun (ya'ni chiziqlar ) paradoks yuzaga kelmaydi, chunki n = 1 so n2 = 1 < n(n + 3) / 2 = 2. Umuman olganda ikkita aniq chiziq L1 va L2 bitta nuqtada kesishadi P agar chiziqlar teng gradyanli (nishabli) bo'lmasa, u holda ular umuman kesishmaydi. Chiziqni aniqlash uchun bitta nuqta etarli emas (ikkitasi kerak); nuqta orqali P u erda nafaqat berilgan ikkita satr, balki cheksiz ko'p qatorlar ham o'tadi.
Xuddi shunday ikkita notekis konus konikslari maksimal tekislikning to'rtta chekkasida eng ko'p kesishadi, bu 3 dan kam2 Bézout teoremasi bilan maksimal qiymat sifatida berilgan 9, va notekis konusni aniqlash uchun 5 ball kerak.
Kub egri chiziqlar uchun Kramerning misoli
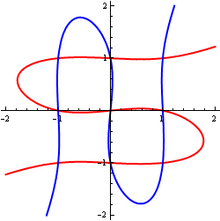
Eylerga yozgan xatida Kramer kubik egri chiziqlarga egaligini ta'kidlagan x3 − x = 0 va y3 − y = 0 aniq 9 nuqtada kesishadi (har bir tenglama uchta parallel chiziqlar to'plamini ifodalaydi x = −1, x = 0, x = +1; va y = −1, y = 0, y Tegishlicha = +1). Shunday qilib, bu kabi buzilgan holatlarda kubik egri chiziqni yagona aniqlash uchun 9 ball etarli emas.
Qaror
Ikki darajali tenglama n 1 + ga ega n(n + 3) / 2 koeffitsienti, lekin tenglama koeffitsientlardan biriga bo'linib, bitta koeffitsient 1 ga teng bo'lib qolsa va tenglama bilan tavsiflangan nuqtalar to'plami saqlanib qoladi n(n + 3) / 2 egri chiziqni tavsiflovchi koeffitsientlar. Berilgan n(n + 3) / 2 ball (xmen, ymen), ushbu nuqtalarning har biri uni darajadagi umumiy polinom tenglamasiga almashtirish orqali alohida tenglama yaratish uchun ishlatilishi mumkin. n, berib n(n + 3) / 2 dagi chiziqli tenglamalar n(n + 3) / 2 noma'lum koeffitsientlar. Agar bu tizim nolga teng bo'lmagan ma'noda buzilmasa aniqlovchi, noma'lum koeffitsientlar noyob tarzda aniqlanadi va shuning uchun polinom tenglamasi va uning egri chizig'i yagona aniqlanadi. Ammo agar bu determinant nolga teng bo'lsa, tizim buzilgan va nuqtalar bir nechta daraja egri chizig'ida bo'lishi mumkin n.
Adabiyotlar
- ^ a b Vayshteyn, Erik V. "Kramer-Eyler paradoksi". MathWorld-dan - Wolfram veb-resursi. http://mathworld.wolfram.com/Cramer-EulerParadox.html
- ^ Maklaurin, Kolin (1720). Geometria Organica. London.
- ^ Tvidi, Charlz (1891 yil yanvar). "V. - Kolin Maklaurinning" Geometria Organica ": tarixiy va tanqidiy tadqiqot". Edinburg qirollik jamiyatining operatsiyalari. 36 (1–2): 87–150. Olingan 28 sentyabr 2012.
- ^ a b Struik, D. J. (1969). Matematikadan manbaviy kitob, 1200-1800. Garvard universiteti matbuoti. p. 182. ISBN 0674823559.
- ^ Tvidi, Charlz (1915). "Kolin Maklaurinning hayoti va yozuvlarini o'rganish". Matematik gazeta. 8 (119): 133–151. JSTOR 3604693.
- ^ Euler, L. "Sur une contricious apparente dans la doctrine des lignes courbes." Berlin Mémoires de l'Académie des Sciences 4, 219-233, 1750
