G2 (matematika) - G2 (mathematics)
| Algebraik tuzilish → Guruh nazariyasi Guruh nazariyasi |
|---|
 |
Asosiy tushunchalar |
Cheksiz o'lchovli yolg'on guruhi
|
| Yolg'on guruhlar |
|---|
 |
|
Yilda matematika, G2 uchta oddiy ism Yolg'on guruhlar (murakkab shakl, ixcham haqiqiy shakl va bo'lingan haqiqiy shakl), ularning Yolg'on algebralar shuningdek, ba'zilari algebraik guruhlar. Ular beshta istisnolardan eng kichigi oddiy Lie guruhlari. G2 2 daraja va 14 o'lchovga ega. Ikkita asosiy vakolatxonalar, 7 va 14 o'lchamlari bilan.
G.ning ixcham shakli2 deb ta'riflash mumkin avtomorfizm guruhi ning oktonion algebra yoki teng ravishda, 8-o'lchovli har qanday tanlangan ma'lum bir vektorni saqlaydigan SO (7) kichik guruhi sifatida haqiqiy spinor vakillik (a spin vakili ).
Tarix
Yolg'on algebra , eng kichik oddiy Lie algebrasi bo'lib, ulardan birinchisi, oddiy Lie algebralarini tasniflashga urinish paytida topilgan. 1887 yil 23 mayda, Vilgelm o'ldirish ga xat yozdi Fridrix Engel u hozir biz chaqiradigan 14 o'lchovli oddiy Lie algebrasini topganini aytdi .[1]
1893 yilda, Élie Cartan ochiq to'plamni tavsiflovchi yozuvni nashr etdi 2 o'lchovli bilan jihozlangan tarqatish - ya'ni, teginish fazosining 2 o'lchovli pastki bo'shliqlarining silliq o'zgaruvchan maydoni - buning uchun Lie algebrasi cheksiz simmetriya sifatida paydo bo'ladi.[2] Xuddi shu yili, xuddi shu jurnalda Engel xuddi shu narsani payqadi. Keyinchalik aniqlanishicha, 2 o'lchovli taqsimot boshqa to'pga o'ralgan to'p bilan chambarchas bog'liq. Yuvarlanan koptokning konfiguratsiya maydoni 5 o'lchovli bo'lib, 2 o'lchovli taqsimot bilan koptok siljish yoki burilishsiz aylanayotgan harakatlarini tavsiflaydi.[3][4]
1900 yilda Engel 7 o'lchovli kompleks vektor makonidagi umumiy antisimetrik uch chiziqli shakl (yoki 3 shakl) G ning murakkab shakliga izomorf guruh tomonidan saqlanib qolishini aniqladi.2.[5]
1908 yilda Kartan oktonionlarning avtomorfizm guruhi 14 o'lchovli oddiy Lie guruhi ekanligini ta'kidladi.[6] 1914 yilda u G ning ixcham haqiqiy shakli ekanligini aytdi2.[7]
Eski kitoblarda va qog'ozlarda G2 ba'zan E bilan belgilanadi2.
Haqiqiy shakllar
Ushbu ildiz tizimiga oid 3 ta oddiy Lie algebralari mavjud:
- Kompleks Lie algebra G ning asosiy yotgan algebrasi2 28-o'lchovga ega. U tashqi avtomorfizm sifatida murakkab konjugatsiyaga ega va shunchaki bog'langan. U bilan bog'langan guruhning maksimal ixcham kichik guruhi G ning ixcham shakli hisoblanadi2.
- Yilni algebra 14 o'lchovli. Bog'langan Lie guruhi tashqi avtomorfizmga, markazga ega emas va shunchaki bog'langan va ixchamdir.
- Kompakt bo'lmagan (bo'lingan) shaklning Lie algebrasi 14-o'lchovga ega. Bog'langan oddiy Lie guruhi 2-tartibli asosiy guruhga ega va uning tashqi avtomorfizm guruhi ahamiyatsiz guruh. Uning maksimal ixcham kichik guruhi SU (2) × SU (2) / (- 1, -1). Unda oddiygina bog'langan algebraik bo'lmagan ikki qavatli qopqoq bor.
Algebra
Dynkin diagrammasi va karton matritsasi
The Dynkin diagrammasi uchun G2 tomonidan berilgan ![]() .
.
Uning Kartan matritsasi bu:
G ning ildizlari2
 12 vektor ildiz tizimi G.2 2 o'lchamda. | 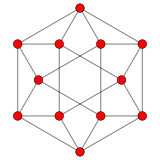 A2 Kokseter tekisligi ning 12 vertikasining proektsiyasi kuboktaedr bir xil 2D vektor tartibini o'z ichiga oladi. | 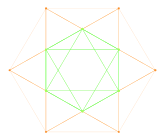 Kokseter tekisligiga proektsiyalangan F4 va E8 kichik guruhi sifatida G2 grafigi |
Garchi ular oraliq chizilgan kabi 2 o'lchovli bo'shliq, ularni ko'rib chiqish ancha nosimmetrikdir vektorlar uch o'lchovli kosmosning 2 o'lchovli pastki fazosida.
|
|
Bitta to'plam oddiy ildizlar, uchun ![]()
![]()
![]() bu:
bu:
- (0,1,−1), (1,−2,1)
Veyl / Kokseter guruhi
Uning Veyl /Kokseter guruh bo'ladi dihedral guruh, ning buyurtma 12. Bu minimal sodiq darajaga ega .
Maxsus holonomiya
G2 kabi paydo bo'lishi mumkin bo'lgan maxsus guruhlardan biridir holonomiya a guruhi Riemann metrikasi. The manifoldlar G.2 holonomiya ham deyiladi G2- ko'p qatlamli.
Polinom o'zgarmas
G2 kommutativ bo'lmagan o'zgaruvchilar tarkibidagi quyidagi ikki polinomning avtomorfizm guruhidir.
- (± almashtirishlar)
oktonion algebrasidan kelib chiqadi. O'zgaruvchilar komutativ bo'lmagan bo'lishi kerak, aks holda ikkinchi polinom bir xil nolga teng bo'ladi.
Generatorlar
Koeffitsientli 14 generatorning vakolatxonasini qo'shish A, ..., N matritsani beradi:
Bu aynan guruhning algebrasi
Vakolatxonalar
Haqiqiy va murakkab Lie algebralari va Lie guruhlarining cheklangan o'lchovli tasvirlari belgilarining barchasi Weyl belgilar formulasi. Eng kichik qisqartirilmaydigan tasvirlarning o'lchamlari (ketma-ketlik) A104599 ichida OEIS ):
- 1, 7, 14, 27, 64, 77 (ikki marta), 182, 189, 273, 286, 378, 448, 714, 729, 748, 896, 924, 1254, 1547, 1728, 1729, 2079 (ikki marta), 2261, 2926, 3003, 3289, 3542, 4096, 4914, 4928 (ikki marta), 5005, 5103, 6630, 7293, 7371, 7722, 8372, 9177, 9660, 10206, 10556, 11571, 11648, 12096, 13090….
14 o'lchovli vakillik bu qo'shma vakillik, va 7 o'lchovli G ning harakati2 xayoliy oktoniyalarda.
77, 2079, 4928, 28652 va boshqalarning ikkita izomorf bo'lmagan qisqartirilmaydigan tasvirlari mavjud. asosiy vakolatxonalar o'lchamlari 14 va 7 ga teng bo'lganlar (ikkita tugunga to'g'ri keladi Dynkin diagrammasi uchlik o'q birinchisidan ikkinchisiga yo'naltiradigan tartibda).
Vogan (1994) G ning bo'linib ketgan haqiqiy shaklining (cheksiz o'lchovli) unitar qisqartirilmaydigan tasvirlarini tasvirlab berdi2.
Cheklangan guruhlar
G guruhi2(q) algebraik guruhning G nuqtalari2 ustidan cheklangan maydon Fq. Ushbu cheklangan guruhlar birinchi tomonidan taqdim etilgan Leonard Eugene Dickson yilda Dikson (1901) g'alati uchun q va Dikson (1905) hatto uchun q. G. tartibi2(q) q6(q6 − 1)(q2 − 1). Qachon q ≠ 2, guruh oddiy va qachon q = 2, uning oddiy kichik guruhi mavjud indeks 2 ga izomorfik 2A2(32), va oktonionlarning maksimal tartibidagi avtomorfizm guruhidir. Janko guruhi J1 birinchi G ning kichik guruhi sifatida qurilgan2(11). Ri (1960) buralgan holda kiritilgan Ree guruhlari 2G2(q) buyurtma q3(q3 + 1)(q − 1) uchun q = 32n+1, toq kuch 3 ga teng.
Shuningdek qarang
- Kartan matritsasi
- Dynkin diagrammasi
- Iordaniya algebrasi
- Asosiy vakillik
- G2-tuzilma
- Yolg'on guruh
- Etti o'lchovli o'zaro faoliyat mahsulot
- Simple Lie guruhi
Adabiyotlar
- ^ Agrikola, Ilka (2008). "Istisno guruhda eski va yangi G2" (PDF). Amerika Matematik Jamiyati to'g'risida bildirishnomalar. 55 (8): 922–929. JANOB 2441524.
- ^ Élie Cartan (1893). "Sur la structure des groupes simples finis et continus". C. R. Akad. Ilmiy ish. 116: 784–786.
- ^ Gil Bor va Richard Montgomeri (2009). "G2 va "prokat tarqatish""". L'Enseignement Mathématique. 55: 157–196. arXiv:matematik / 0612469. doi:10.4171 / lem / 55-1-8.
- ^ John Baez va John Huerta (2014). "G2 va dumaloq to'p ". Trans. Amer. Matematika. Soc. 366 (10): 5257–5293. arXiv:1205.2447. doi:10.1090 / s0002-9947-2014-05977-1.
- ^ Fridrix Engel (1900). "Ein neues, dem linearen Kompleks analoglari Gebilde". Leyps. Ber. 52: 63–76, 220–239.
- ^ Élie Cartan (1908). "Nombres majmualari". Matematika fanlari ensiklopediyasi. Parij: Gautier-Villars. 329-468 betlar.
- ^ Élie Cartan (1914), "Les groupes reels simples finis et continus", Ann. Ilmiy ish. École Norm. Sup., 31: 255–262
- Adams, J. Frank (1996), Istisno yolg'on guruhlari bo'yicha ma'ruzalar, Matematikadan Chikago ma'ruzalari, Chikago universiteti matbuoti, ISBN 978-0-226-00526-3, JANOB 1428422
- Baez, Jon (2002), "Oktonionlar", Buqa. Amer. Matematika. Soc., 39 (2): 145–205, arXiv:matematik / 0105155, doi:10.1090 / S0273-0979-01-00934-X.
- 4.1 bo'limiga qarang: G2; HTML-ning onlayn versiyasi mavjud http://math.ucr.edu/home/baez/octonions/node14.html.
- Bryant, Robert (1987), "Favqulodda holonomiya ko'rsatkichlari", Matematika yilnomalari, 2, 126 (3): 525–576, doi:10.2307/1971360, JSTOR 1971360
- Dikson, Leonard Eugene (1901), "Ixtiyoriy maydonda chiziqli guruhlar nazariyasi", Amerika Matematik Jamiyatining operatsiyalari, Providence, R.I .: Amerika matematik jamiyati, 2 (4): 363–394, doi:10.1090 / S0002-9947-1901-1500573-3, ISSN 0002-9947, JSTOR 1986251, To'plagan hujjatlarining II jildida qayta nashr etilgan Leonard E. Dikson G guruhlari haqida xabar berdi2 g'alati xarakterli sohalarda.
- Dikson, L. E. (1905), "Oddiy guruhlarning yangi tizimi", Matematika. Ann., 60: 137–150, doi:10.1007 / BF01447497 Leonard E. Dikson G guruhlari haqida xabar berdi2 hatto xarakterli sohalarda.
- Ri, Rimxak (1960), "oddiy Lie algebra turiga bog'liq bo'lgan oddiy guruhlar oilasi (G)2)", Amerika Matematik Jamiyati Axborotnomasi, 66 (6): 508–510, doi:10.1090 / S0002-9904-1960-10523-X, ISSN 0002-9904, JANOB 0125155
- Vogan, kichik Devid A. (1994), "G.ning unitar duali2", Mathematicae ixtirolari, 116 (1): 677–791, Bibcode:1994InMat.116..677V, doi:10.1007 / BF01231578, ISSN 0020-9910, JANOB 1253210




![{ displaystyle left [{ begin {array} {rr} 2 & -3 - 1 & 2 end {array}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37b6638e3fd0ff7eab3058d40fed0f592c94dbf4)







