Barqaror tarqatish - Stable distribution

Barqaror

Ehtimollar zichligi funktsiyasi Nosimmetrik a- o'lchov koeffitsienti bilan barqaror taqsimotlar Birlik shkalasi koeffitsienti bilan egri markazlashtirilgan barqaror taqsimotlar
Kümülatif taqsimlash funktsiyasi Nosimmetrik uchun CDF a- barqaror taqsimotlar 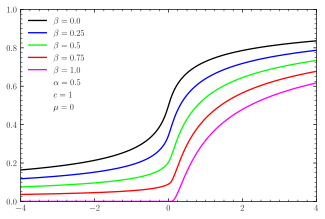Eğimli markazlashtirilgan barqaror tarqatish uchun CDFlar
Parametrlar	a b (0, 2] - barqarorlik parametri β ∈ [−1, 1] - skewness parametri (e'tibor bering qiyshiqlik aniqlanmagan) v ∈ (0, ∞) — o'lchov parametri m ∈ (−∞, ∞) - joylashish parametri
Qo'llab-quvvatlash	x ∈ [m, + ∞) agar a <1 va b = 1 x ∈ (-∞, m], agar a <1 va ph = -1 x ∈ R aks holda
PDF	ba'zi parametr qiymatlari bundan mustasno, analitik jihatdan tushunarli emas
CDF	ba'zi parametr qiymatlari bundan mustasno, analitik jihatdan tushunarli emas
Anglatadi	m qachon a> 1, aks holda aniqlanmagan
Median	m qachon b = 0, aks holda analitik jihatdan tushunarli emas
Rejim	m qachon b = 0, aks holda analitik jihatdan tushunarli emas
Varians	2v2 qachon a = 2, aks holda cheksiz
Noqulaylik	0 qachon a = 2, aks holda aniqlanmagan
Ex. kurtoz	0 qachon a = 2, aks holda aniqlanmagan
Entropiya	ba'zi parametr qiymatlari bundan mustasno, analitik jihatdan tushunarli emas
MGF	${ displaystyle exp ! chap (t mu + c ^ {2} t ^ {2} o'ng)}$ qachon ${ displaystyle alpha = 2}$, aks holda aniqlanmagan
CF	${ displaystyle exp ! { Big [} ; it mu - | c , t | ^ { alpha} , (1-i beta operator nomi {sgn} (t) Phi) ; { Katta]},}$ qayerda ${ displaystyle Phi = { begin {case} tan { tfrac { pi alpha} {2}} & { text {if}} alpha neq 1 - { tfrac {2} { pi}} log | c , t | & { text {if}} alpha = 1 end {case}}}$

Yilda ehtimollik nazariyasi, a tarqatish deb aytilgan barqaror agar a chiziqli birikma ikkitadan mustaqil tasodifiy o'zgaruvchilar ushbu taqsimot bilan bir xil taqsimot mavjud, qadar Manzil va o'lchov parametrlar. Tasodifiy o'zgaruvchi deyiladi barqaror agar uning taqsimoti barqaror bo'lsa. Barqaror taqsimot oilasi ba'zan ba'zan deb ham ataladi Levi alfa-barqaror taqsimoti, keyin Pol Levi, uni o'rgangan birinchi matematik.^[1][2]

Oilani belgilaydigan to'rt parametrdan asosan barqarorlik parametri a ga e'tibor qaratildi (panelga qarang). Barqaror taqsimotlarda 0 normal taqsimot, va a = 1 ga Koshi taqsimoti. Tarqatishlar aniqlanmagan dispersiya a <2 uchun va aniqlanmagan anglatadi a ≤ uchun 1. Barqaror ehtimollik taqsimotining ahamiyati shundaki, ular "attraktorlar "to'g'ri normalangan mustaqil va bir xil taqsimlangan summalar uchun (iid ) tasodifiy o'zgaruvchilar. Oddiy taqsimot barqaror taqsimot oilasini belgilaydi. Klassik tomonidan markaziy chegara teoremasi har biri cheklangan dispersiyali tasodifiy o'zgaruvchilar to'plamining to'g'ri normalangan yig'indisi o'zgaruvchilar sonining ko'payishi bilan normal taqsimotga intiladi. Cheklangan dispersiya taxminisiz chegara normal bo'lmagan barqaror taqsimot bo'lishi mumkin. Mandelbrot "barqaror paretian taqsimotlari" deb nomlangan taqsimotlarga,^[3][4][5] keyin Vilfredo Pareto. Xususan, u 1 [1] u odatdagi taqsimotlarga qaraganda aktsiyalar va tovarlarning narxlarini yaxshiroq ta'rifi deb bilgan.^[6]

Ta'rif

Yo'qdegenerativ tarqalish agar u quyidagi xususiyatni qondirsa, barqaror taqsimot hisoblanadi:

Ruxsat bering X₁ va X₂ a-ning mustaqil nusxalari bo'lishi mumkin tasodifiy o'zgaruvchi X. Keyin X deb aytilgan barqaror har qanday doimiy uchun bo'lsa a > 0 va b > 0 tasodifiy o'zgaruvchi aX₁ + bX₂ bilan bir xil taqsimotga ega cX + d ba'zi bir doimiy uchun v > 0 va d. Tarqatish deyilgan qat'iy barqaror agar bu ushlab turilsa d = 0.^[7]

Beri normal taqsimot, Koshi taqsimoti, va Levi tarqatish barchasi yuqoridagi xususiyatga ega, shundan kelib chiqadiki, ular barqaror taqsimlanishning alohida holatlari.

Bunday taqsimotlar to'rt parametrli doimiy oilani tashkil qiladi ehtimollik taqsimoti m va shkala parametrlari bilan parametrlangan vmos ravishda va mos ravishda assimetriya va kontsentratsiya o'lchovlariga mos keladigan ikkita shakl parametrlari b va a (rasmlarga qarang).

The xarakterli funktsiya φ (t) har qanday ehtimollik taqsimotining faqat Furye konvertatsiyasi uning ehtimollik zichligi funktsiyasi f (x). Shuning uchun zichlik funktsiyasi xarakterli funktsiyani teskari Furye konversiyasidir.^[8]

${ displaystyle f (x) = { frac {1} {2 pi}} int _ {- infty} ^ { infty} varphi (t) e ^ {- ixt} , dt}$

Umumiy barqaror taqsimot uchun ehtimollik zichligi funktsiyasini analitik usulda yozib bo'lmasada, umumiy xarakterli funktsiyani analitik tarzda ifodalash mumkin. Tasodifiy o'zgaruvchi X xarakterli funktsiyasini quyidagicha yozish mumkin bo'lsa, barqaror deyiladi^[7][9]

${ displaystyle varphi (t; alfa, beta, c, mu) = exp left (it mu - | ct | ^ { alpha} chap (1-i beta operator nomi {sgn} (t) Phi o'ng) o'ng)}$

qaerda sgn (t) faqat imzo ning t va

${ displaystyle Phi = { begin {case} tan left ({ frac { pi alpha} {2}} right) & alpha neq 1 - { frac {2} { pi}} log | t | & alpha = 1 end {case}}}$

m ∈ R shift ∈ [−1, 1] ga o'tish parametrlari, deb nomlanadi skewness parametri, assimetriya o'lchovidir. E'tibor bering, bu doirada odatiy qiyshiqlik yaxshi aniqlanmagan, chunki a <2 uchun taqsimot 2 yoki undan yuqori darajani tan olmaydi lahzalar va odatiy skewness ta'rifi 3-chi markaziy moment.

Buning barqaror taqsimot berishining sababi shundaki, ikkita tasodifiy o'zgaruvchining yig'indisi uchun xarakteristik funktsiya mos keladigan ikkita xarakterli funktsiya mahsulotiga teng. Barqaror taqsimotdan ikkita tasodifiy o'zgaruvchini qo'shganda a va b qiymatlari bir xil, lekin ehtimol m va v.

Har bir funktsiya qonuniy ehtimollik taqsimotining o'ziga xos funktsiyasi emas (ya'ni kimningdir) kümülatif taqsimlash funktsiyasi haqiqiy va 0 dan 1 gacha kamaymasdan boradi), lekin parametrlar ularning diapazonida bo'lguncha yuqorida keltirilgan xarakterli funktsiyalar qonuniy bo'ladi. Xarakteristik funktsiyalarning ma'lum bir qiymatdagi qiymati t uning qiymatining murakkab konjugatidir -t ehtimollarni taqsimlash funktsiyasi haqiqiy bo'lishi uchun shunday bo'lishi kerak.

Β = 0 oddiy holatda xarakteristik funktsiya shunchaki a kengaytirilgan eksponent funktsiya; taqsimot m ga nisbatan nosimmetrik va (Lévy) deb nomlanadi nosimmetrik alfa-barqaror taqsimot, ko'pincha qisqartiriladi SAS.

A <1 va ph = 1 bo'lganda, taqsimot [m, ph) tomonidan qo'llab-quvvatlanadi.

Parametr v > 0 - bu o'lchov koeffitsienti, bu tarqatish kengligining o'lchovidir, a esa tarqatishning ko'rsatkichi yoki ko'rsatkichi bo'lib, tarqatishning asimptotik harakatini belgilaydi.

Parametrlar

Yuqoridagi ta'rif barqaror taqsimot uchun ishlatiladigan parametrlardan faqat bittasi; u eng keng tarqalgan, lekin at parametrlarida doimiy emas a = 1.

Uzluksiz parametrlash^[7]

${ displaystyle varphi (t; alfa, beta, gamma, delta) = exp left (it delta - | gamma t | ^ { alpha} left (1-i beta operatorname {sgn} (t) Phi right) right)}$

qaerda:

${ displaystyle Phi = { begin {case} left (| gamma t | ^ {1- alpha} -1 right) tan left ({ tfrac { pi alpha} {2}} right) & alpha neq 1 - { frac {2} { pi}} log | gamma t | & alpha = 1 end {case}}}$

A va b diapazonlari oldingi kabi, γ (o'xshash) v) musbat, δ (m kabi) esa haqiqiy bo'lishi kerak.

Har qanday parametrlashda tasodifiy o'zgaruvchini zichligi teng bo'lgan tasodifiy o'zgaruvchini olish uchun chiziqli o'zgartirishni amalga oshirish mumkin ${ displaystyle f (y; alpha, beta, 1,0)}$. Birinchi parametrlashda bu yangi o'zgaruvchini aniqlash orqali amalga oshiriladi:

${ displaystyle y = { begin {case} { frac {x- mu} { gamma}} & alfa neq 1 { frac {x- mu} { gamma}} - beta { frac {2} { pi}} ln gamma & alpha = 1 end {case}}}$

Ikkinchi parametrlash uchun biz shunchaki foydalanamiz

${ displaystyle y = { frac {x- delta} { gamma}}.}$

a nima bo'lishidan qat'iy nazar. Birinchi parametrlashda, agar o'rtacha qiymat mavjud bo'lsa (ya'ni, a > 1) u $ m $ ga teng, ikkinchi parametrlashda o'rtacha mavjud bo'lganda u $ ga teng ${ displaystyle delta - beta gamma tan left ({ tfrac { pi alpha} {2}} right).}$

Tarqatish

Shuning uchun barqaror taqsimot yuqoridagi to'rt parametr bilan belgilanadi. Har qanday degeneratsiyalanmagan barqaror taqsimotning zich (cheksiz farqlanadigan) zichlik funktsiyasiga ega ekanligini ko'rsatish mumkin.^[7] Agar ${ displaystyle f (x; alfa, beta, c, mu)}$ zichligini bildiradi X va Y ning mustaqil nusxalari yig'indisidir X:

${ displaystyle Y = sum _ {i = 1} ^ {N} k_ {i} (X_ {i} - mu) ,}$

keyin Y zichlikka ega ${ displaystyle s ^ {- 1} f (y / s; alfa, beta, c, 0)}$ bilan

${ displaystyle s = left ( sum _ {i = 1} ^ {N} | k_ {i} | ^ { alpha} right) ^ { frac {1} { alpha}}.}$

Asimptotik xatti-harakatlar a <2 uchun quyidagicha tavsiflanadi:^[7]

${ displaystyle f (x) sim { frac {1} {| x | ^ {1+ alpha}}}} left (c ^ { alpha} (1+ operatorname {sgn} (x) beta) ) sin chap ({ frac { pi alpha} {2}} o'ng) { frac { Gamma ( alfa +1)} { pi}} o'ng)}$

bu erda Γ Gamma funktsiyasi (bundan tashqari) a ≥ 1 va β = ± 1, dumi chapga yoki o'ngga g'oyib bo'lmaydi, resp., Of m, yuqoridagi ifoda 0) bo'lsa ham. Bu "og'ir dum "xatti-harakatlar barqaror taqsimotlarning tafovutini hamma uchun cheksiz bo'lishiga olib keladi a <2. Ushbu xususiyat quyidagi log-log uchastkalarida ko'rsatilgan.

Qachon a = 2, taqsimot Gauss (pastga qarang), quyruqlari asimptotik ekspozitsiya bilan (-x²/4v²) / (2c√π).

Bir tomonlama barqaror taqsimot va barqaror sonli taqsimot

A <1 va ph = 1 bo'lganda, taqsimot [m, ph) tomonidan qo'llab-quvvatlanadi. Ushbu oila deyiladi bir tomonlama barqaror taqsimot.^[10] Uning standart taqsimoti (m = 0) quyidagicha aniqlanadi

${ displaystyle L _ { alpha} (x) = f chap (x; alfa, 1, cos left ({ frac { alpha pi} {2}} right) ^ {1 / alpha }, 0 o'ng)}$, qayerda ${ displaystyle alfa <1}$.

Ruxsat bering ${ displaystyle q = exp (-i alfa pi / 2)}$, uning xarakterli vazifasi ${ displaystyle varphi (t; alfa) = exp left (-q | t | ^ { alpha} o'ng)}$. Shunday qilib, uning PDF-ning ajralmas shakli quyidagicha (eslatma: ${ displaystyle { text {Im}} (q) <0}$)

${ displaystyle { begin {aligned} L _ { alpha} (x) & = { frac {1} { pi}} Re left [ int _ {- infty} ^ { infty} e ^ {itx} e ^ {- q | t | ^ { alpha}} , dt right] & = { frac {2} { pi}} int _ {0} ^ { infty} e ^ {- { text {Re}} (q) , t ^ { alfa}} sin (tx) sin (- { text {Im}} (q) , t ^ { alpha}) , dt, { text {or}} & = { frac {2} { pi}} int _ {0} ^ { infty} e ^ {- { text {Re}} (q ) , t ^ { alpha}} cos (tx) cos ({ text {Im}} (q) , t ^ { alpha}) , dt. end {hizalanmış}}}$

Ikki sinusli integral juda kichik uchun samaraliroq ${ displaystyle x}$.

Levi summasini ko'rib chiqing ${ displaystyle Y = sum _ {i = 1} ^ {N} X_ {i}}$ qayerda ${ displaystyle X_ {i} sim L _ { alpha} (x)}$, keyin Y zichlikka ega ${ displaystyle { frac {1} { nu}} L _ { alpha} chap ({ frac {x} { nu}} o'ng)}$ qayerda ${ displaystyle nu = N ^ {1 / alfa}}$. O'rnatish ${ displaystyle x = 1}$, biz yetib boramiz barqaror hisoblash taqsimoti.^[11] Uning standart taqsimoti quyidagicha aniqlanadi

${ displaystyle { mathfrak {N}} _ { alpha} ( nu) = { frac { alpha} { Gamma left ({ frac {1} { alpha}} right)}} { frac {1} { nu}} L _ { alfa} chap ({ frac {1} { nu}} o'ng)}$, qayerda ${ displaystyle nu> 0}$ va ${ displaystyle alfa <1}$.

Barqaror hisoblash taqsimoti oldingi konjugat bir tomonlama barqaror taqsimot. Uning joylashuvi bo'yicha oilasi quyidagicha aniqlanadi

${ displaystyle { mathfrak {N}} _ { alpha} ( nu; nu _ {0}, theta) = { frac { alpha} { Gamma ({ frac {1} { alpha) }})}} { frac {1} { nu - nu _ {0}}} L _ { alfa} chap ({ frac { theta} { nu - nu _ {0}}} o'ng)}$, qayerda ${ displaystyle nu> nu _ {0}}$, ${ displaystyle theta> 0}$va ${ displaystyle alfa <1}$.

Bundan tashqari, tomonidan qo'llab-quvvatlanadigan bir tomonlama tarqatish ${ displaystyle [ nu _ {0}, infty)}$. Joylashuv parametri ${ displaystyle nu _ {0}}$ kesilgan joy, esa ${ displaystyle theta}$ uning ko'lamini belgilaydi.

Qachon ${ displaystyle alpha = { frac {1} {2}}}$, ${ displaystyle L _ { frac {1} {2}} (x)}$ bo'ladi Levi tarqatish bu teskari gamma taqsimoti. Shunday qilib ${ displaystyle { mathfrak {N}} _ { frac {1} {2}} ( nu; nu _ {0}, theta)}$ siljigan gamma taqsimoti shakli 3/2 va shkalasi ${ displaystyle 4 theta}$,

${ displaystyle { mathfrak {N}} _ { frac {1} {2}} ( nu; nu _ {0}, theta) = { frac {1} {4 { sqrt { pi }} theta ^ {3/2}}} ( nu - nu _ {0}) ^ {1/2} e ^ {- { frac { nu - nu _ {0}} {4 teta}}}}$, qayerda ${ displaystyle nu> nu _ {0}}$, ${ displaystyle theta> 0}$.

Uning o'rtacha qiymati ${ displaystyle nu _ {0} +6 theta}$ va uning standart og'ishi ${ displaystyle { sqrt {24}} theta}$. Bu taxmin qilingan VIX kabi tarqatiladi ${ displaystyle { mathfrak {N}} _ { frac {1} {2}} ( nu; nu _ {0}, theta)}$ bilan ${ displaystyle nu _ {0} = 10.4}$ va ${ displaystyle theta = 1.6}$ (7-bo'limga qarang ^[11]). Shunday qilib barqaror hisoblash taqsimoti o'zgaruvchanlik jarayonining birinchi darajali marginal taqsimoti. Shu nuqtai nazardan, ${ displaystyle nu _ {0}}$ "qavatning o'zgaruvchanligi" deb nomlanadi.

Barqaror hisoblash taqsimotini olishning yana bir yondashuvi bir tomonlama barqaror taqsimotning Laplas konvertatsiyasidan foydalanishdir (2.4-bo'lim ^[11])

${ displaystyle int _ {0} ^ { infty} e ^ {- zx} L _ { alpha} (x) dx = e ^ {- z ^ { alpha}}}$, qayerda ${ displaystyle alfa <1}$.

Ruxsat bering ${ displaystyle x = 1 / nu}$, va chap tomonda joylashgan integralni a sifatida ajratish mumkin mahsulotni taqsimlash standart Laplas taqsimoti va standart barqaror hisoblash taqsimoti,

${ displaystyle int _ {0} ^ { infty} { frac {1} { nu}} chap ({ frac {1} {2}} e ^ {- { frac {| z |} { nu}}} o'ng) chap ({ frac { alfa} { Gamma ({ frac {1} { alfa}})}}} { frac {1} { nu}} L_ { alfa} ({ frac {1} { nu}}) o'ng) d nu = { frac {1} {2}} { frac { alpha} { Gamma ({ frac {1} { alfa}})}} e ^ {- | z | ^ { alfa}}}$, qayerda ${ displaystyle alfa <1}$.

Bunga "lambda dekompozitsiyasi" deyiladi (4-bo'limga qarang.) ^[11]) chunki o'ng tomoni Lihnning avvalgi asarlarida "simmetrik lambda taqsimoti" deb nomlangan. Biroq, uning "kabi bir nechta mashhur nomlari boreksponent quvvatni taqsimlash ", yoki" umumiy xato / normal taqsimot ", ko'pincha a> 1 bo'lganda aytiladi.

N-chi lahzasi ${ displaystyle { mathfrak {N}} _ { alpha} ( nu)}$ bo'ladi ${ displaystyle - (n + 1)}$- ning momenti ${ displaystyle L _ { alpha} (x)}$, Barcha ijobiy daqiqalar cheklangan. Bu qaysidir ma'noda turg'un taqsimotdagi turlicha momentlar masalasini hal qiladi.

Xususiyatlari

• Barcha barqaror taqsimotlar cheksiz bo'linadigan.
• Bundan mustasno normal taqsimot (a = 2), barqaror taqsimotlar leptokurtotik va og'ir dumaloq taqsimotlar.
• Konvolyutsiyada yopish

Barqaror taqsimotlar konvertatsiya ostida a ning belgilangan qiymati uchun yopiladi. Konvolyutsiya Fyureyga o'zgartirilgan funktsiyani ko'paytirishga teng bo'lganligi sababli, bir xil a ga ega bo'lgan ikkita barqaror xarakterli funktsiyalarning ko'paytmasi yana shunday xarakterli funktsiyani beradi. Ikkita barqaror xarakterli funktsiyalarning mahsuloti quyidagicha:

${ displaystyle exp left (it mu _ {1} + it mu _ {2} - | c_ {1} t | ^ { alpha} - | c_ {2} t | ^ { alpha} + i beta _ {1} | c_ {1} t | ^ { alfa} operator nomi {sgn} (t) Phi + i beta _ {2} | c_ {2} t | ^ { alfa} operator nomi {sgn} (t) Phi o'ng)}$

$ D $ $ m $ funktsiyasi emasligi sababli, v yoki β o'zgaruvchilardan kelib chiqadiki, biriktirilgan funktsiya uchun ushbu parametrlar quyidagicha berilgan:

${ displaystyle { begin {aligned} mu & = mu _ {1} + mu _ {2} | c | & = left (| c_ {1} | ^ { alpha} + | c_ {2} | ^ { alpha} right) ^ { frac {1} { alpha}} [6pt] beta & = { frac { beta _ {1} | c_ {1} | ^ { alfa} + beta _ {2} | c_ {2} | ^ { alpha}} {| c_ {1} | ^ { alpha} + | c_ {2} | ^ { alfa}}}} oxiri {hizalanmış}}}$

Har holda, natijada parametrlarning barqaror taqsimlash uchun zarur bo'lgan vaqt oralig'ida bo'lishini ko'rsatish mumkin.

Umumlashtirilgan markaziy chegara teoremasi

Ushbu bo'lim uchun qo'shimcha iqtiboslar kerak tekshirish. Iltimos yordam bering ushbu maqolani yaxshilang tomonidan ishonchli manbalarga iqtiboslarni qo'shish. Ma'lumot manbasi bo'lmagan material shubha ostiga olinishi va olib tashlanishi mumkin. (May 2020) (Ushbu shablon xabarini qanday va qachon olib tashlashni bilib oling)

Barqaror taqsimotlarning yana bir muhim xususiyati bu ularning umumlashtirilgan rolidir markaziy chegara teoremasi. Markaziy chegara teoremasi shuni ko'rsatadiki, cheklangan nolga teng bo'lmagan bir qator mustaqil va bir xil taqsimlangan (i.i.d) tasodifiy o'zgaruvchilar yig'indisi a ga intiladi. normal taqsimot o'zgaruvchilar soni o'sib borishi bilan.

Tufayli bir umumlashtirish Gnedenko va Kolmogorov nosimmetrik taqsimotga ega bo'lgan tasodifiy o'zgaruvchilar sonining kuch-qonun quyruqlariga ega ekanligi (Paretiya dumlari ) kabi kamayadi ${ displaystyle | x | ^ {- alfa -1}}$ qayerda ${ displaystyle 0 < alpha leqslant 2}$ (va shuning uchun cheksiz farqga ega), barqaror taqsimotga moyil bo'ladi ${ displaystyle f (x; alfa, 0, c, 0)}$ chaqiriqlar soni o'sib borishi bilan.^[12] Agar ${ displaystyle alpha> 2}$ unda yig'indisi barqarorlik parametri 2 ga teng bo'lgan barqaror taqsimotga, ya'ni Gauss taqsimotiga yaqinlashadi.^[13]

Boshqa imkoniyatlar ham mavjud. Masalan, tasodifiy o'zgaruvchining xarakterli funktsiyasi to-ga asimptotik bo'lsa ${ displaystyle 1 + a | t | ^ { alpha} ln | t |}$ kichik uchun t (ijobiy yoki salbiy), keyin qanday qilib so'rashimiz mumkin t bilan o'zgaradi n xarakteristik funktsiya yig'indisi uchun qiymati qachon n bunday tasodifiy o'zgaruvchilar berilgan qiymatga teng siz:

${ displaystyle varphi _ { text {sum}} = varphi ^ {n} = u}$

Bir lahzani taxmin qilsak t → 0, yuqoridagi chegarani quyidagicha qabul qilamiz n → ∞:

${ displaystyle ln u = lim _ {n to infty} n ln varphi = lim _ {n to infty} na | t | ^ { alpha} ln | t |.}$

Shuning uchun:

${ displaystyle { begin {aligned} ln ( ln u) & = ln left ( lim _ {n to infty} na | t | ^ { alpha} ln | t | right) [5pt] & = lim _ {n to infty} ln chap (na | t | ^ { alpha} ln | t | o'ng) = lim _ {n to infty} chap { ln (na) + alfa ln | t | + ln ( ln | t |) right } end {hizalangan}}}$

Bu shuni ko'rsatadiki ${ displaystyle ln | t |}$ uchun asimptotik ${ displaystyle { tfrac {-1} { alpha}} ln n,}$ biz oldingi tenglamadan foydalanib

${ displaystyle | t | sim chap ({ frac {- alpha ln u} {na ln n}} right) ^ {1 / alpha}.}$

Bu shuni anglatadiki, yig'indiga bo'linadi

${ displaystyle chap ({ frac {na ln n} { alpha}} o'ng) ^ { frac {1} { alpha}}}$

xarakterli funktsiyaga ega, uning qiymati ba'zi qiymatlarda t ′ boradi siz (kabi n ortadi) qachon ${ displaystyle t '= (- ln u) ^ { frac {1} { alpha}}.}$ Boshqacha qilib aytganda, xarakterli funktsiya yo'naltirilgan tomonga yaqinlashadi ${ displaystyle exp (- (t ') ^ { alfa})}$ va shuning uchun Levining davomiyligi teoremasi yig'indisi

${ displaystyle chap ({ frac {na ln n} { alpha}} o'ng) ^ { frac {1} { alpha}}}$

tarqatishda birlashadi barqarorlik parametri bilan nosimmetrik alfa-barqaror taqsimotga ${ displaystyle alpha}$ va parametr 1.

Buni dumlari sifatida kamayadigan tasodifiy o'zgaruvchiga qo'llash mumkin ${ displaystyle | x | ^ {- 3}}$. Ushbu tasodifiy o'zgaruvchining o'rtacha qiymati, ammo dispersiyasi cheksizdir. Keling, quyidagi taqsimotni olaylik:

${ displaystyle f (x) = { begin {case} { frac {1} {3}} & | x | leqslant 1 { frac {1} {3}} x ^ {- 3} & | x |> 1 end {holatlar}}}$

Biz buni quyidagicha yozishimiz mumkin

${ displaystyle f (x) = int _ {1} ^ { infty} { frac {2} {w ^ {4}}} h chap ({ frac {x} {w}} o'ng) dw}$

qayerda

${ displaystyle h left ({ frac {x} {w}} right) = { begin {case} { frac {1} {2}} & left | { frac {x} {w} } o'ng | <1, 0 va chap | { frac {x} {w}} o'ng |> 1. end {holatlar}}}$

Biz xarakterli funktsiyani asimptotik kengayishining etakchi shartlarini topmoqchimiz. Ehtimollar taqsimotining xarakterli funktsiyasi ${ displaystyle { tfrac {1} {w}} h chap ({ tfrac {x} {w}} o'ng)}$ bu ${ displaystyle { tfrac { sin (tw)} {tw}},}$ shuning uchun xarakterli funktsiya f(x)

${ displaystyle varphi (t) = int _ {1} ^ { infty} { frac {2 sin (tw)} {tw ^ {4}}} dw}$

va biz hisoblashimiz mumkin:

${ displaystyle { begin {aligned} varphi (t) -1 & = int _ {1} ^ { infty} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} - 1 right] , dw & = int _ {1} ^ { frac {1} {| t |}} { frac {2} {w ^ { 3}}} chap [{ frac { sin (tw)} {tw}} - 1 o'ng] , dw + int _ { frac {1} {| t |}} ^ { infty} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} - 1 right] , dw & = int _ {1} ^ { frac {1} {| t |}} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} - 1+ left {- { frac {t ^ {2} w ^ {2}} {3!}} + { frac {t ^ {2} w ^ {2}} {3!}} right } right] , dw + int _ { frac {1} {| t |}} ^ { infty} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw }} - 1 right] , dw & = int _ {1} ^ { frac {1} {| t |}} - { frac {t ^ {2} dw} {3w}} + int _ {1} ^ { frac {1} {| t |}} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} -1 + { frac {t ^ {2} w ^ {2}} {3!}} Right] dw + int _ { frac {1} {| t |}} ^ { infty} { frac {2} {w ^ {3}}} chap [{ frac { sin (tw)} {tw}} - 1 o'ng] dw & = int _ {1} ^ { frac {1 } {| t |}} - { frac {t ^ {2} dw} {3w}} + left { int _ {0} ^ { frac {1} {| t |}} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} - 1 + { frac {t ^ {2} w ^ {2}} {3!} } o'ng] dw- int _ {0} ^ {1} { frac {2} {w ^ {3 }}} left [{ frac { sin (tw)} {tw}} - 1 + { frac {t ^ {2} w ^ {2}} {3!}} right] dw right } + int _ { frac {1} {| t |}} ^ { infty} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} { tw}} - 1 right] dw & = int _ {1} ^ { frac {1} {| t |}} - { frac {t ^ {2} dw} {3w}} + t ^ {2} int _ {0} ^ {1} { frac {2} {y ^ {3}}} left [{ frac { sin (y)} {y}} - 1 + { frac {y ^ {2}} {6}} right] dy- int _ {0} ^ {1} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} - 1 + { frac {t ^ {2} w ^ {2}} {6}} right] dw + t ^ {2} int _ {1} ^ { infty } { frac {2} {y ^ {3}}} chap [{ frac { sin (y)} {y}} - 1 o'ng] dy & = - { frac {t ^ { 2}} {3}} int _ {1} ^ { frac {1} {| t |}} { frac {dw} {w}} + t ^ {2} C_ {1} - int _ {0} ^ {1} { frac {2} {w ^ {3}}} chap [{ frac { sin (tw)} {tw}} - 1 + { frac {t ^ {2} w ^ {2}} {6}} right] dw + t ^ {2} C_ {2} & = { frac {t ^ {2}} {3}} ln | t | + t ^ {2} C_ {3} - int _ {0} ^ {1} { frac {2} {w ^ {3}}} left [{ frac { sin (tw)} {tw}} - 1 + { frac {t ^ {2} w ^ {2}} {6}} right] dw & = { frac {t ^ {2}} {3}} ln | t | + t ^ {2} C_ {3} - int _ {0} ^ {1} { frac {2} {w ^ {3}}} left [{ frac {t ^ {4} w ^ {4} } {5!}} + Cdots right] dw & = { frac {t ^ {2}} {3}} ln | t | + t ^ {2} C_ {3} - { mathcal {O}} chap (t ^ {4} o'ng) end {al bekor qilindi}}}$

qayerda ${ displaystyle C_ {1}, C_ {2}}$ va ${ displaystyle C_ {3}}$ doimiydir. Shuning uchun,

${ displaystyle varphi (t) sim 1 + { frac {t ^ {2}} {3}} ln | t |}$

va yuqorida aytilganlarga ko'ra (va bu o'zgaruvchanligi f(x; 2,0,1,0) 2), yig'indisi n bo'linadigan ushbu tasodifiy o'zgaruvchining misollari ${ displaystyle { sqrt {n ( ln n) / 12}},}$ taqsimotda Gauss taqsimotiga dispersiya bilan yaqinlashadi. Ammo har qanday aniqlikdagi dispersiya n hali ham cheksiz bo'ladi. Chegaralanuvchi taqsimotning kengligi tasodifiy o'zgaruvchining cheklangan dispersiyasiga ega bo'lgan holatga qaraganda tezroq o'sishiga e'tibor bering (bu holda kenglik n). The o'rtacha, yig'indini bo'linish yo'li bilan olingan n, kengligi nolga yaqinlashgan Gauss tomon harakat qiladi n ga mos ravishda ortadi Katta sonlar qonuni.

Maxsus holatlar

Katta kuch kuchini ko'rsatadigan nosimmetrik markazlashtirilgan barqaror tarqatish PDF-larining log-log uchastkasi x. Quvvat qonuni xatti-harakatlari katta hajmdagi PDF-ning to'g'ri chiziqli ko'rinishi bilan tasdiqlanadi x, Nishab - (a + 1) ga teng. (Faqatgina istisno odatdagi taqsimot bo'lgan qora rangdagi a = 2 uchun.)

Quvvat qonuni xatti-harakatlarini aks ettiruvchi PDF-larning egri markazlashtirilgan barqaror taqsimotining log-log uchastkasi x. Yana chiziqli qismlarning qiyaligi - (a + 1) ga teng

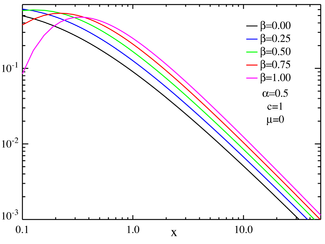
Formasi uchun umumiy analitik echim mavjud emas p(x). Biroq, uchta maxsus holat mavjud bo'lib, ular bilan ifodalanishi mumkin elementar funktsiyalar buni tekshirish orqali ko'rish mumkin xarakterli funktsiya:^[7][9][14]

• A = 2 uchun taqsimot a ga kamayadi Gauss taqsimoti dispersiyasi bilan σ² = 2v² va o'rtacha m; skewness parametri β ta'sir qilmaydi.
• A = 1 va ph = 0 uchun taqsimot a ga kamayadi Koshi taqsimoti o'lchov parametri bilan v va o'zgaruvchan parametr m.
• A = 1/2 va ph = 1 uchun taqsimot a ga kamayadi Levi tarqatish o'lchov parametri bilan v va o'zgaruvchan parametr m.

E'tibor bering, yuqoridagi uchta taqsimot ham quyidagi tarzda bog'langan: Koshi standart tasodifiy o'zgaruvchisini a sifatida ko'rish mumkin aralash Gauss tasodifiy o'zgaruvchilarining (barchasi o'rtacha nolga teng), dispersiyasi standart Leviy taqsimotidan kelib chiqqan holda. Aslida bu umumiy teoremaning maxsus hodisasidir (59-betga qarang) ^[15]) har qanday nosimmetrik alfa-barqaror taqsimotni shu tarzda ko'rib chiqishga imkon beradi (aralashma taqsimotining alfa parametri aralashtirish taqsimotining alfa parametrining ikki baravariga teng bo'lsa va aralashtirish taqsimotining beta parametri har doim bittaga teng bo'lsa).

A ning oqilona qiymatlari bilan barqaror PDF-lar uchun umumiy yopiq shakl ifodasi mavjud Meijer G-funktsiyalari.^[16] Fox H-funktsiyalari barqarorlik zichligi funktsiyalarini ifodalash uchun ham ishlatilishi mumkin. Oddiy ratsional sonlar uchun yopiq shakl ifodasi ko'pincha unchalik murakkab bo'lmagan holda bo'ladi maxsus funktsiyalar. Maxsus funktsiyalar bo'yicha juda sodda ifodalarga ega bo'lgan bir nechta yopiq shaklli iboralar mavjud. Quyidagi jadvalda PDF elementar funktsiyalar bilan ifodalanadigan E va maxsus funktsiyalar bilan ifodalanadiganlar an bilan belgilanadi s.^[15]

Ba'zi maxsus holatlar ma'lum nomlar bilan ma'lum:

• A = 1 va ph = 1 uchun taqsimot a ga teng Landau tarqatish ushbu nom ostida fizikada o'ziga xos foydalanishga ega.
• A = 3/2 va ph = 0 uchun taqsimot a ga kamayadi Holtsmark tarqatish o'lchov parametri bilan v va o'zgaruvchan parametr m.

Bundan tashqari, sifatida v nolga yaqinlashadi yoki a nolga yaqinlashganda taqsimot a ga yaqinlashadi Dirac delta funktsiyasi δ(x − m).

Seriyani namoyish qilish

Barqaror taqsimot oddiyroq integralning haqiqiy qismi sifatida qayta ko'rib chiqilishi mumkin:^[17]

${ displaystyle f (x; alpha, beta, c, mu) = { frac {1} { pi}} Re left [ int _ {0} ^ { infty} e ^ {it (x- mu)} e ^ {- (ct) ^ { alfa} (1-i beta Phi)} , dt right].}$

Ikkinchi eksponentni a sifatida ifodalash Teylor seriyasi, bizda ... bor:

${ displaystyle f (x; alpha, beta, c, mu) = { frac {1} { pi}} Re left [ int _ {0} ^ { infty} e ^ {it (x- mu)} sum _ {n = 0} ^ { infty} { frac {(-qt ^ { alpha}) ^ {n}} {n!}} , dt right]}$

qayerda ${ displaystyle q = c ^ { alfa} (1-i beta Phi)}$. Integratsiya va yig'indining tartibini bekor qilish va integratsiyani amalga oshirish:

${ displaystyle f (x; alfa, beta, c, mu) = { frac {1} { pi}} Re left [ sum _ {n = 1} ^ { infty} { frac {(-q) ^ {n}} {n!}} chap ({ frac {i} {x- mu}} o'ng) ^ { alfa n + 1} Gamma ( alfa n + 1) o'ng]}$

uchun amal qiladi x ≠ m va parametrlarning mos qiymatlari uchun yaqinlashadi. (E'tibor bering n = 0 atama, natijada a hosil bo'ladi delta funktsiyasi yilda xShuning uchun thereforem tushirib qo'yilgan.) Birinchi eksponentni ketma-ketlik bilan ifodalash ijobiy kuchlarda yana bir qator hosil qiladi x−m, bu odatda unchalik foydali emas.

Bir tomonlama barqaror taqsimot uchun yuqoridagi qator kengayishini o'zgartirish kerak, chunki ${ displaystyle q = exp (-i alfa pi / 2)}$ va ${ displaystyle qi ^ { alpha} = 1}$. Xulosa qilishning haqiqiy qismi yo'q. Buning o'rniga xarakteristik funktsiyani integrali salbiy o'qda bajarilishi kerak, bu esa quyidagilarni beradi:^[18][10]

${ displaystyle { begin {aligned} L _ { alpha} (x) & = { frac {1} { pi}} Re left [ sum _ {n = 1} ^ { infty} { frac {(-q) ^ {n}} {n!}} chap ({ frac {-i} {x}} o'ng) ^ { alfa n + 1} Gamma ( alfa n + 1) right] & = { frac {1} { pi}} sum _ {n = 1} ^ { infty} { frac {- sin (n ( alfa +1) pi)} {n!}} chap ({ frac {1} {x}} o'ng) ^ { alpha n + 1} Gamma ( alfa n + 1) end {hizalangan}}}$

Barqaror o'zgaruvchilarni simulyatsiya qilish

Barqaror tasodifiy o'zgaruvchilar ketma-ketligini simulyatsiya qilish oddiy emas, chunki teskari uchun analitik ifodalar mavjud emas ${ displaystyle F ^ {- 1} (x)}$ na CDF ${ displaystyle F (x)}$ o'zi.^[19][11] Rad etish yoki inversiya usullari kabi barcha standart yondashuvlar zerikarli hisob-kitoblarni talab qiladi. Chambers, Mallows and Stuck (CMS) tomonidan ancha oqlangan va samarali echim taklif qilingan,^[20] kim ma'lum bir integral formulani ko'rgan^[21] quyidagi algoritmni berdi:^[22]

• tasodifiy o'zgaruvchini yaratish ${ displaystyle U}$ bir xil taqsimlangan ${ displaystyle chap (- { tfrac { pi} {2}}, { tfrac { pi} {2}} o'ng)}$ va mustaqil eksponentli tasodifiy miqdor ${ displaystyle W}$ o'rtacha 1 bilan;
• uchun ${ displaystyle alpha neq 1}$ hisoblash:

${ displaystyle X = chap (1+ zeta ^ {2} o'ng) ^ { frac {1} {2 alpha}} { frac { sin ( alpha (U + xi))}} {( cos (U)) ^ { frac {1} { alfa}}}} chap ({ frac { cos (U- alfa (U + xi))}} {W}} right) ^ { frac {1- alpha} { alfa}},}$

• uchun ${ displaystyle alpha = 1}$ hisoblash:

${ displaystyle X = { frac {1} { xi}} left { left ({ frac { pi} {2}} + beta U right) tan U- beta log chap ({ frac {{ frac { pi} {2}} W cos U} {{ frac { pi} {2}} + beta U}} right) right },}$

qayerda

${ displaystyle zeta = - beta tan { frac { pi alpha} {2}}, qquad xi = { begin {case} {{frac {1} { alpha}} arctan ( - zeta) & alpha neq 1 { frac { pi} {2}} & alpha = 1 end {case}}}$

Ushbu algoritm tasodifiy o'zgaruvchini beradi ${ displaystyle X sim S _ { alpha} ( beta, 1,0)}$. Batafsil dalil uchun qarang.^[23]

Standart barqaror tasodifiy o'zgaruvchini simulyatsiya qilish formulalarini hisobga olgan holda, biz parametrlarning barcha qabul qilingan qiymatlari uchun barqaror tasodifiy o'zgaruvchini osongina taqlid qilishimiz mumkin ${ displaystyle alpha}$, ${ displaystyle c}$, ${ displaystyle beta}$ va ${ displaystyle mu}$ quyidagi xususiyatdan foydalangan holda. Agar ${ displaystyle X sim S _ { alpha} ( beta, 1,0)}$ keyin

${ displaystyle Y = { begin {case} cX + mu & alpha neq 1 cX + { frac {2} { pi}} beta c log c + mu & alpha = 1 end { holatlar}}}$

bu ${ displaystyle S _ { alpha} ( beta, c, mu)}$. Uchun ${ displaystyle alpha = 2}$ (va ${ displaystyle beta = 0}$) CMS usuli taniqli darajaga kamayadi Box-Myuller konvertatsiyasi ishlab chiqarish uchun Gauss tasodifiy o'zgaruvchilar.^[24] Adabiyotda ko'plab boshqa yondashuvlar, jumladan Bergström va LePage qatorlarini kengaytirishni taklif qilishgan ^[25] va,^[26] navbati bilan. Biroq, CMS usuli eng tezkor va eng aniq deb hisoblanadi.

Ilovalar

Barqaror taqsimotlar nazariyani ham, amaliyotda ham ularning ahamiyatini umumlashtirish uchun qarzdor markaziy chegara teoremasi ikkinchi (va ehtimol birinchi) tartibsiz tasodifiy o'zgaruvchilarga lahzalar va unga hamrohlik qiladi o'ziga o'xshashlik barqaror oila. Bu odatiylikdan chiqib ketish va moliyaviy ma'lumotlar uchun o'ziga o'xshash modelga bo'lgan talab (ya'ni yillik aktivlar narxining o'zgarishi uchun taqsimot shakli har kunlik yoki oylik narx o'zgaruvchilariga o'xshash bo'lishi kerak) sabab bo'ldi. Benoit Mandelbrot paxta narxlari alfa-barqaror taqsimotga muvofiq, a 1,7 ga teng.^[6] Levi tarqatish tahlilida tez-tez uchraydi tanqidiy xatti-harakatlar va moliyaviy ma'lumotlar.^[9][27]

Ular, shuningdek, topilgan spektroskopiya kvazistatik jihatdan umumiy ifoda sifatida bosim kengaygan spektral chiziq.^[17]

Quyosh nurlarini kutish vaqtini (alevlanish hodisalari orasidagi vaqtni) Lévy taqsimoti namoyish etildi CGRO 2001 yil dekabr oyida BATSE qattiq rentgen nurlari alanga oldi. Levining statistik imzosini tahlil qilish natijasida ikki xil xotira imzosi aniq bo'lganligi aniqlandi; biri quyosh tsikli bilan bog'liq, ikkinchisi kelib chiqishi lokalizatsiya qilingan yoki mahalliy faol quyosh ta'sirining kombinatsiyasi bilan bog'liq ko'rinadi.^[28]

Boshqa analitik holatlar

Analitik ko'rinadigan barqaror taqsimotlarning bir qator holatlari ma'lum. Barqaror taqsimot quyidagicha ifodalansin ${ displaystyle f (x; alfa, beta, c, mu)}$ keyin bilamiz:

• The Cauchy Distribution tomonidan berilgan ${ displaystyle f (x; 1,0,1,0).}$
• The Levi tarqatish tomonidan berilgan ${ displaystyle f (x; { tfrac {1} {2}}, 1,1,0).}$
• The Oddiy taqsimot tomonidan berilgan ${ displaystyle f (x; 2,0,1,0).}$
• Ruxsat bering ${ displaystyle S _ { mu, nu} (z)}$ bo'lishi a Lommel funktsiyasi, keyin:^[29]

${ displaystyle f chap (x; { tfrac {1} {3}}, 0,1,0 o'ng) = Re chap ({ frac {2e ^ {- { frac {i pi} {4}}}} {3 { sqrt {3}} pi}} { frac {1} { sqrt {x ^ {3}}}} S_ {0, { frac {1} {3} }} chap ({ frac {2e ^ { frac {i pi} {4}}} {3 { sqrt {3}}}} { frac {1} { sqrt {x}}} o'ng) o'ng)}$

• Ruxsat bering ${ displaystyle S (x)}$ va ${ displaystyle C (x)}$ ni belgilang Frenel integrallari keyin:^[30]

${ displaystyle f chap (x; { tfrac {1} {2}}, 0,1,0 o'ng) = { frac {1} { sqrt {2 pi | x | ^ {3}} }} chap ( sin chap ({ tfrac {1} {4 | x |}} o'ng) chap [{ frac {1} {2}} - S chap ({ tfrac {1} { sqrt {2 pi | x |}}} o'ng) o'ng] + cos chap ({ tfrac {1} {4 | x |}} o'ng) chap [{ frac {1} {2}} - C chap ({ tfrac {1} { sqrt {2 pi | x |}}} o'ng) o'ng] o'ng)}$

• Ruxsat bering ${ displaystyle K_ {v} (x)}$ bo'lishi o'zgartirilgan Bessel funktsiyasi keyin ikkinchi turdagi:^[30]

${ displaystyle f chap (x; { tfrac {1} {3}}, 1,1,0 o'ng) = { frac {1} { pi}} { frac {2 { sqrt {2 }}} {3 ^ { frac {7} {4}}}} { frac {1} { sqrt {x ^ {3}}}} K _ { frac {1} {3}} chap ( { frac {4 { sqrt {2}}} {3 ^ { frac {9} {4}}}} { frac {1} { sqrt {x}}} right)}$

• Agar ${ displaystyle {} _ {m} F_ {n}}$ ni belgilang gipergeometrik funktsiyalar keyin:^[29]

${ displaystyle { begin {aligned} f left (x; { tfrac {4} {3}}, 0,1,0 right) & = { frac {3 ^ { frac {5} {4 }}} {4 { sqrt {2 pi}}}} { frac { Gamma chap ({ tfrac {7} {12}} o'ng) Gamma chap ({ tfrac {11} {) 12}} o'ng)} { Gamma chap ({ tfrac {6} {12}} o'ng) Gamma chap ({ tfrac {8} {12}} o'ng)}} {} _ { 2} F_ {2} chapga ({ tfrac {7} {12}}, { tfrac {11} {12}}; { tfrac {6} {12}}, { tfrac {8} {12) }}; { tfrac {3 ^ {3} x ^ {4}} {4 ^ {4}}} o'ng) - { frac {3 ^ { frac {11} {4}} x ^ {3 }} {4 ^ {3} { sqrt {2 pi}}}} { frac { Gamma chap ({ tfrac {13} {12}} o'ng) Gamma chap ({ tfrac {) 17} {12}} o'ng)} { Gamma chap ({ tfrac {18} {12}} o'ng) Gamma chap ({ tfrac {15} {12}} o'ng)}} { } _ {2} F_ {2} chap ({ tfrac {13} {12}}, { tfrac {17} {12}}; { tfrac {18} {12}}, { tfrac {15) } {12}}; { tfrac {3 ^ {3} x ^ {4}} {4 ^ {4}}} o'ng) [6pt] f left (x; { tfrac {3} { 2}}, 0,1,0 o'ng) va = { frac { Gamma chap ({ tfrac {5} {3}} o'ng)} { pi}} {} _ {2} F_ { 3} chap ({ tfrac {5} {12}}, { tfrac {11} {12}}; { tfrac {1} {3}}, { tfrac {1} {2}}, { tfrac {5} {6}}; - { tfrac {2 ^ {2} x ^ {6}} {3 ^ {6}}} o'ng) - { frac {x ^ {2}} {3 pi}} {} _ {3} F_ {4} l eft ({ tfrac {3} {4}}, 1, { tfrac {5} {4}}; { tfrac {2} {3}}, { tfrac {5} {6}}, { tfrac {7} {6}}, { tfrac {4} {3}}; - { tfrac {2 ^ {2} x ^ {6}} {3 ^ {6}}} right) + { frac {7x ^ {4} Gamma chap ({ tfrac {4} {3}} o'ng)} {3 ^ {4} pi ^ {2}}} {} _ {2} F_ {3} chap ({ tfrac {13} {12}}, { tfrac {19} {12}}; { tfrac {7} {6}}, { tfrac {3} {2}}, { tfrac) {5} {3}}; - { tfrac {2 ^ {2} x ^ {6}} {3 ^ {6}}} right) end {aligned}}}$

ikkinchisi esa Holtsmark tarqatish.

• Ruxsat bering ${ displaystyle W_ {k, mu} (z)}$ bo'lishi a Whittaker funktsiyasi, keyin:^[31][32][33]

${ displaystyle { begin {aligned} f left (x; { tfrac {2} {3}}, 0,1,0 right) & = { frac { sqrt {3}} {6 { sqrt { pi}} | x |}} exp chap ({ tfrac {2} {27}} x ^ {- 2} o'ng) W _ {- { frac {1} {2}}, { frac {1} {6}}} chap ({ tfrac {4} {27}} x ^ {- 2} o'ng) [8pt] f chap (x; { tfrac {2} { 3}}, 1,1,0 o'ng) & = { frac { sqrt {3}} {{ sqrt { pi}} | x |}} exp left (- { tfrac {16} {27}} x ^ {- 2} o'ng) W _ {{ frac {1} {2}}, { frac {1} {6}}} chap ({ tfrac {32} {27}} x ^ {- 2} o'ng) [8pt] f chap (x; { tfrac {3} {2}}, 1,1,0 o'ng) & = { begin {case} {{frac { sqrt {3}} {{ sqrt { pi}} | x |}} exp left ({ frac {1} {27}} x ^ {3} right) W _ {{ frac { 1} {2}}, { frac {1} {6}}} chap (- { frac {2} {27}} x ^ {3} o'ng) va x <0 {} { frac { sqrt {3}} {6 { sqrt { pi}} | x |}} exp left ({ frac {1} {27}} x ^ {3} right) W _ {- { frac {1} {2}}, { frac {1} {6}}} chap ({ frac {2} {27}} x ^ {3} right) va x geq 0 end { holatlar}} end {hizalangan}}}$

Shuningdek qarang

• Levi parvozi
• Levi jarayoni
• Fraksiyonel kvant mexanikasi
• Boshqa "kuch qonuni" tarqatish
  • Pareto tarqatish
  • Zeta tarqatish
  • Zipf tarqatish
  • Zipf - Mandelbrot tarqatish
• O'zgaruvchanlik klasteri bilan barqaror va temperaturali barqaror taqsimotlar - moliyaviy dasturlar
• Ko'p o'zgaruvchan barqaror taqsimot
• Diskret-barqaror taqsimot

Izohlar

• Windows uchun STABLE dasturi Jon Nolanning barqaror veb-sahifasida mavjud: http://academic2.american.edu/~jpnolan/stable/stable.html. U umumiy barqaror taqsimot uchun zichlikni (pdf), kümülatif taqsimlash funktsiyasini (cdf) va kvantillarni hisoblab chiqadi va barqaror parametrlarning maksimal taxminiy bahosini va ma'lumotlar to'plamining mosligini baholash uchun ba'zi ma'lumotlarni tahlil qilish usullarini bajaradi.
• libstable a C barqaror tarqatish pdf, cdf, tasodifiy son, kvantile va fitting funktsiyalari uchun amal qilish (benchmark replikatsiya to'plami va R to'plami bilan birga).
• R Paket "barqaror" Diethelm Vuertz, Martin Maechler va Rmetrics asosiy jamoasi a'zolari tomonidan. Barqaror zichlik, ehtimollik, kvantil va tasodifiy sonlarni hisoblab chiqadi. 2016 yil 12 sentyabrda yangilangan.

Adabiyotlar